|
|
Universidade Federal de Campina Grande Departamento de Sistemas e Computação Disciplina: Introdução à Programação –
Turma: 03 Período: 2016.1 – Prof. Roberto Faria 3ª.
Lista de Exercícios - Preparação para a 2ª. Prova DATA:
06/09/2015 |
Data
Limite de Entrega: 13/09/2016
E-mail
de Entrega: ip.t3.exercicios@gmail.com
Responder todos os exercícios e entregar até
a data limite:
1)
Diz-se que um número inteiro é um número
perfeito se a soma de seus fatores, incluindo 1 (mas não o numero em si),
resulta no próprio número. Por exemplo, 6 é um número perfeito porque 6 = 1 + 2
+ 3. Escreva uma função perfeito que determine se o parâmetro numero é
um número perfeito. Use essa função
em um programa que determine e imprima todos os números perfeitos entre 1 e N.
Imprima os fatores de cada número encontrado para confirmar que ele é realmente
perfeito. Desafie o poder de seu computador testando números muito maiores do
que 1000.
2) O máximo
divisor comum (MDC) de dois inteiros é o maior inteiro que divide
precisamente cada um dos dois números. Escreva um programa que leia N pares de
inteiros e mostre o MDC de cada par, utilizando uma função mdc que
retorna o máximo divisor comum de dois inteiros.
3) Escreva
um programa que simule o lançamento de uma moeda. Para cada lançamento da
moeda, o programa deve imprimir Cara ou Coroa. Deixe o programa lançar a moeda
100 vezes e conte o número de vezes que cada lado da moeda aparece. Imprima os
resultados. O programa deve chamar uma função separada jogada que não utiliza argumentos e retorna 0 para coroa e 1 para
cara.
Nota: Se
o programa simular realisticamente o lançamento da moeda, cada lado da moeda
deve aparecer aproximadamente metade do tempo, totalizando cerca de 50 caras e
50 coroas.
4) Os
computadores estão desempenhando um papel cada vez maior em educação. Escreva
um programa que ajudará os alunos da escola do primeiro grau a aprender a
multiplicar. Use rand para produzir dois inteiros positivos de um
dígito. O programa deve então imprimir uma pergunta do tipo Quanto e 6 vezes
7? O aluno deve digitar a resposta. Seu programa deve examinar a resposta
do aluno. Se ela estiver correta, o programa deve imprimir "Muito bem!"
e fazer outra pergunta de multiplicação. Se a resposta estiver errada, o
programa deve imprimir "Nao. Tente novamente, por favor." e
então deixar que o aluno fique tentando acertar a mesma pergunta repetidamente
até por fim conseguir.
5)
A série de Fibonacci:
0,
1, 1, 2, 3, 5, 8, 13, 21, ...
começa
com os termos 0 e 1 e tem a propriedade de que cada termo subsequente ser a
soma dos dois termos precedentes. Escreva um programa que utilize uma função não-recursiva fibonacci (n) que calcula o n-ésimo
número de Fibonacci.
6)
Escreva um programa que use uma função distancia
que calcula a distância entre os pontos de vários pares de pontos (x1, y1)
e (x2, y2). Todos os números e valores de retorno devem ser do tipo float. O programa encerra quando x1 igual a x2 e
y1 igual a y2.
7)
(Torres
de Hanói) Todo cientista computacional principiante deve lidar com
determinados problemas clássicos, e o problema das Torres de Hanói (veja a figura
a seguir) é um dos mais famosos. Diz a lenda que em um templo do Extremo
Oriente os sacerdotes estão tentando mover uma pilha de discos de um pino para
outro. A pilha inicial tinha 64 discos colocados em um pino e organizados na
ordem decrescente, da base para o topo. Os sacerdotes estão tentando mover a pilha
desse pino para um segundo pino com a restrição de que exatamente um disco deve
ser movido de cada vez e em nenhum momento um disco maior pode ser colocado
sobre um disco menor. Há um terceiro pino disponível para colocação temporária
de discos. Teoricamente o mundo terminará quando os sacerdotes completarem sua
tarefa, portanto há pouco estímulo para facilitarmos seus esforços. Vamos
assumir que os sacerdotes estão tentando mover os discos do pino 1 para o pino
3. Desejamos desenvolver um algoritmo que imprimirá a sequência exata de
transferências dos discos de um pino para outro. Se fossemos solucionar este
problema com os métodos convencionais, rapidamente nos encontraríamos perdidos
lidando com os discos. Em vez disso, se solucionarmos o problema com recursividade
em mente, ele se torna imediatamente viável. Mover n discos pode ser
considerado em termos de mover apenas n - I discos (daí a recursão) como
se segue:
- Mova n - 1 discos do pino
I para o pino 2. usando o pino 3 como área de armazenamento temporário.
- Mova o último disco (o maior) do
pino 1 para o pino 3.
3.
Mova
os n - 1 discos do pino 2 para o pino 3. usando o pino 1 como área de armazenamento
temporário.
O
processo termina quando a última tarefa envolver mover n = 1 disco,
i.e., o caso básico. Isso é realizado movendo simplesmente o disco para o seu
destino final, sem a necessidade de uma área de armazenamento temporário. Escreva
um programa para resolver o problema das Torres de Hanói. Use uma função recursiva
com quatro parâmetros:
- O
número de discos a serem movidos
- O
pino no qual esses discos estão colocados inicialmente
- O
pino para o qual essa pilha de discos deve ser movida
4.
O
pino a ser usado como área de armazenamento temporário
Seu
programa deve imprimir instruções precisas necessárias para mover os discos do pino
inicial para o pino de destino. Por exemplo, para mover uma pilha de três
discos do pino 1 para o pino 3, seu programa deve imprimir a seguinte seqüência
de movimentos:
1
-> 3 (Isso significa mover o disco do pino 1 para o pino 3.)
1
-> 2
3
-> 2
1
-> 3
2
-> 1
2
-> 3
1 -> 3
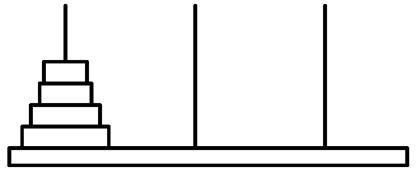
O problema das Torres de Hanói para o caso
com quatro discos.
8) O máximo
divisor comum dos inteiros x e y é o maior inteiro que divide
precisamente x e y. Escreva um programa que use uma função
recursiva mdc que retorne o máximo divisor comum de x e y. O
máximo divisor comum de x e y é definido recursivamente como se
segue: se y for igual a 0, então mdc (x, y) é x; senão, mdc
(x, y) é mdc(y, x % y), onde % é o operador resto (modulus).
OBS: Esses
exercícios são preparação para a segunda prova.
BOM TRABALHO!

