O PETNews deseja agradecer a todos os leitores que enviaram respostas para o desafio do mês passado. Por ordem de recebimento do editor eis os acertadores:

Jaindson Valentim

Flavio Barata

Jemerson Damasio

Abraão Moraes

Leandro José

Fabrício Asfora

Fabiano de Miranda

Pedro Henrique

Resposta da edição passada (Saco de moedas):

RESPOSTA: 83161

Detalhes: Primeiro você tem que calcular o mínimo múltiplo comum entre os números antecessores de 13, ou seja, 2,3,4,5,6,7,8,9,10,11 e 12. Esse número, como você sabe calcular, é 27720. 27720 dividido por 13, dá 2132 e sobram 4. Se acrescentarmos mais 1, vai sobrar 1 quando dividirmos pelos números de 1 a 12, mas vai sobrar 5 quando dividirmos por 13. É fácil adivinhar que o número que for múltiplo de todos teria que ser de forma que quando dividido por 13, sobrasse 12, porque quando acrescentarmos 1 ele ficará múltiplo de 13.
Voltemos ao número 27720, o mmc. Ele é o múltiplo de todos. Mas quando dividimos por 13 dá 4. Queremos que dê 12. Ora, então é só multiplicá-lo por 3, já que 3x4 dá 12. O número fica 3x27720, que dá 83160. Ótimo! 83160 é divisível pelos números de 1 a 12 e dividido por 13 dá 6396 e sobra 12. Basta acrescentar 1, e obtemos 83161, que dividido pelos números de 1 a 12 sobra esse 1, e com certeza é divisível por 13 e dá 6397.

Desafio desse mês (Armadilhas):

Um jogo simples que tem divertido gerações de crianças consiste de um tabuleiro contendo uma trilha de quadrados e um conjunto de peças coloridas. No início do jogo cada jogador recebe uma peça; todas as peças são inicialmente posicionadas imediatamente antes do primeiro quadrado da trilha. O jogo progride em turnos. A cada turno, jogadores jogam um par de dados, e movem suas peças para a frente. As peças são movidas sempre para a frente, pelo número de quadrados correspondente à soma dos pontos obtidos nos dados. A ordem em que os jogadores jogam os dados é sempre a mesma nos turnos (jogador A, depois jogador B, etc.). A maioria dos quadrados da trilha no tabuleiro é “normal”, mas alguns são “armadilhas”. Se a peça de um jogador cai em uma armadilha ao final do movimento de um jogador, o jogador perde a vez de jogar no próximo turno. Ou seja, ele/ela não joga os dados e sua peça fica um turno sem ser movimentada.

Há exatamente três armadilhas na trilha do tabuleiro.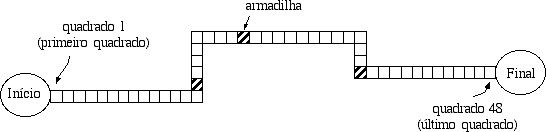

O vencedor do jogo é o jogador cuja peça alcance o final da trilha primeiro. O final da trilha é após o último quadrado da trilha. Considere, por exemplo, o tabuleiro da figura acima, cujos quadrados são numerados de 1 a 48. No início do jogo, as peças estão posicionadas no local marcado “Início” na figura, ou seja, antes do quadrado número 1. Portanto, se um jogador obtém um resultado 7 nos dados (dados marcando 2 e 5, por exemplo), sua peça é posicionada no quadrado número 7 ao final do primeiro turno do jogo. Além do mais, se a peça de um jogador está posicionada no quadrado 41, o jogador necessita de um resultado pelo menos igual a 8 nos dados para alcançar o final da trilha e vencer o jogo. Note ainda que não há empates no jogo.

Sendo fornecidos o número de jogadores, o número de quadrados na trilha, a posição das armadilhas e uma lista de resultados de dados, determine o vencedor do jogo, para os dois casos a seguir.

Obs.: A primeira linha de um caso de teste contém dois inteiros J e Q representando respectivamente o número de jogadores e o número de quadrados na trilha (1 ≤ J ≤ 10 e 3 ≤ Q ≤ 10000). A segunda linha de um caso de teste descreve as armadilhas, representadas por três inteiros distintos T1, T2 e T3, denotando as suas posições na trilha (1 ≤ T1, T2, T3 ≤ Q). A seguir é fornecido o conjunto de resultados dos dados. Cada resultado é descrito em uma linha separada, cada linha contendo inteiros D1 e D2 (1 ≤ D1, D2 ≤ 6), que representam os resultados dos dados. O número de resultados dos dados em um caso de teste será sempre o número exato necessário para que um jogador vença o jogo. Um jogador é identificado por um número de 1 a J. Jogadores jogam em ordem seqüencial, de 1 a J.

• Fevereiro de 2007
• Junho de 2007