

Você já parou para pensar em como funcionam as portas que abrem e fecham automaticamente? E as lavadoras de louça/roupa, termômetros eletrônicos, relógios digitais, calculadoras e máquinas de venda automática? Todos esses dispositivos eletromecânicos têm uma controladora que nada mais é do que um autômato finito.
Além desses dispositivos (controladores), os autômatos finitos também são importantes para reconhecer padrões em dados, como, por exemplo, na análise léxica de um compilador; projetar uma nova linguagem para uma aplicação específica (desenvolvendo seu compilador); processamento de voz; etc.
Um autômato finito é o modelo computacional mais simples e pode ser chamado, também, de máquina de estados finitos. Eles são bons modelos para computadores com uma quantidade de memória extremamente limitada (como é o caso dos dispositivos citados acima).
Tomando como exemplo a porta automática (presente em supermercados, shoppings, etc.), podemos observar na Figura 1 que existe um tapete na frente da porta e outro tapete atrás. Ambos detectam a presença de pessoas prestes a atravessar a passagem, abrindo a porta quando alguém se aproxima e mantendo-a aberta até que a pessoa se afaste.
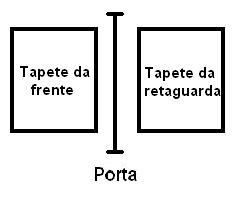
O controlador pode estar em dois estados (aberto ou fechado) e passa de um estado para outro dependendo do estímulo (entrada) que recebe. Nesse caso, tem-se 4 estímulos diferentes: frente (uma pessoa está no tapete da frente); retaguarda (uma pessoa está no tapete de dentro); ambos (há pessoas sobre os dois tapetes) e nenhum (não há ninguém sobre os tapetes). Para cada estímulo, o controlador vai responder de uma forma diferente, realizando as transições de um estado para outro. A representação das possíveis transições de acordo com cada estímulo (chamamos essa representação de diagrama de estados) é apresentada na Figura 2.
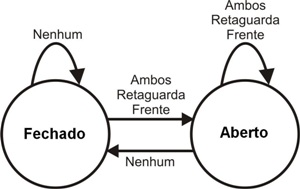
Com o controlador ligado, ao receber a sequência de estímulos frente; retaguarda; nenhum; frente; ambos, tem-se as seguintes transições: fechado (início) -> aberto; aberto -> aberto; aberto -> fechado; fechado -> aberto; aberto -> aberto.
Definindo formalmente, um autômato finito é uma quíntupla < Q, ∑, δ, q0, F >, em que:
- Q é o conjunto finito e não vazio de estados;
- ∑ é um conjunto finito e não vazio chamado alfabeto que indica os símbolos de entrada (no exemplo da porta automática chamamos de estímulos) permitidos;
- δ: Q x ∑ → Q é a função de transição. Essa função recebe um estado e um símbolo de entrada e retorna um estado, definindo, assim, como transitar de um estado para o outro no autômato;
- q0 ∈ Q é o estado inicial;
- F ⊆ Q é o conjunto de estados finais.
Tomando como exemplo o autômato finito M1 = (Q, ∑, δ, q1, F), representado na Figura 3, e definindo-o formalmente, tem-se:
- Q = {q1 , q2 , q3};
- ∑ = {0, 1};
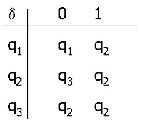
- δ é descrita como
- q1 é o estado inicial;
- F = {q2}.
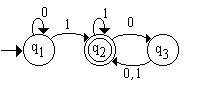
Sabendo que A = ∑* é o conjunto de palavras (cadeias) que o autômato (máquina) M aceita, pode-se estender a função de transição d para δ': Q' x ∑* → Q, em que δ'(q, l) = q; δ'(q, a) = δ(q, a); δ'(q, wa) = δ(δ'(q, w), a). Ou seja, se a função δ'
- recebe como entrada o estado q e uma cadeia vazia (λ): permanece no estado q;
- recebe como entrada o estado q e um símbolo a do alfabeto ∑: tem a mesma transição que δ, recebe o mesmo estado q e o mesmo símbolo a;
- recebe como entrada o estado q e uma cadeia de símbolos de ∑ (wa): tem a mesma transição que δ(δ'(q, w), a). Para entender esse tópico, tome como exemplo o autômato finito M1 (Figura 3) e observe o passo a passo para encontrar o estado resultante da função de transição δ'(q1, 011) abaixo.

Estendendo a função de transição do autômato, é possível reconhecer uma linguagem (no exemplo acima, denominada a linguagem A). Quando uma linguagem A é reconhecida por um autômato M, diz-se que A é linguagem da máquina M e pode ser representada por L(M) = A. No exemplo da Figura 3, o autômato M1 reconhece a linguagem A = {w|w contém pelo menos um 1 e um número par de 0s segue o último 1}.
Considerando um autômato finito M = < Q, ∑, δ, q0, F > e w ∈ ∑*, ou seja, w uma cadeia pertencente à linguagem da máquina, chama-se de computação de M a partir de w uma sequência c0, c1, ..., cn , em que:
- co = < qo, w >
- cn = < qj, λ >, qj ∈ Q
- cj+1= < δ(cj, au), u > , a ∈ ∑ e u ∈ ∑*.
Exemplificando com o autômato M1 (Figura 3), ao realizar a computação de M1 a partir da cadeia 001, tem-se:
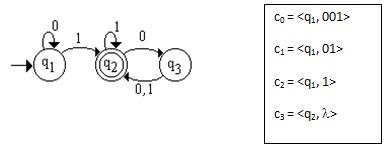
Diz-se que um autômato M aceita uma cadeia w se e somente se existe uma sequência de estados r0, r1, ... , rn tal que:
- r0 = q0 ;
- δ (ri, wi+1) = ri+1 para i = 0, 1, ..., n-1;
- rn ∈ F.
Ou seja, M aceita w se e somente se a computação de M para a entrada w termina em um estado final, ou seja, δ'(q0, w) ∈ F. O conjunto de todas as palavras aceitas por M é chamada de linguagem de M, representada por L(M) = {w ∈ ∑* : δ’(q0, w ) ∈ F}. Uma linguagem reconhecida por um autômato finito é chamada de linguagem regular.
Para exercitar os conceitos vistos neste recapitulando, tente resolver as questões que seguem. Em caso de dúvidas, envie um email para o autor desta matéria.
|
Questão 1 [3]: Considere o autômato finito representado abaixo (note que o estado final está marcado em negrito).
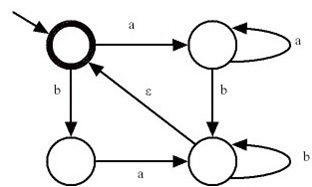 a) Defina formalmente o autômato. b) Determine as computações para as entradas ω 1 = baab, ω 2 = bababa e ω 3 = abaabaa, explicitando se elas são aceitas ou não pelo autômato. c) Determine a linguagem que é reconhecida por este autômato. Questão 2: Escreva um autômato finito qualquer, em sua linguagem de programação preferida. Como base, observe um blog que mostra autômatos finitos em Python aqui. |
Participe do “Recapitulando” enviando-nos sugestões de assuntos que você deseja rever.
Fontes:
[1] SIPSER, Michael. Introdução à Teoria da Computação. 2ª edição. Editora Thomson, 2007.
[2] Slides do Prof. Bernardo Lula Júnior da disciplina Teoria da Computação do período 2005.1.
[3] Lista de exercícios do período 2009.2 aqui.