Desafios pendentes:
Conforme prometido na edição anterior veremos agora as respostas dos desafios de junho e dezembro de 2007.
Junho de 2007: Querida, cheguei!
Se o doutor Barreto chegou 12 minutos mais cedo que o habitual, isso significa que o carro da sua mulher poupou 12 minutos de viagem. Pode-se concluir, portanto, que a viagem entre o ponto em que eles se encontraram e a estação de trem demora seis minutos de carro. Como a caminhada de Barreto é cinco vezes mais lenta que o automóvel, ele passou 30 minutos andando. Assim, se Sandra o tivesse buscado na rodoviária quando o trem chegou, ele teria chegado em casa 24 minutos ainda mais cedo, às 18h36min.
Dezembro/2007: Situação penosa.
A resposta é 300 galinhas. Se “n” for o número de galinhas e “d”, o número de dias de comida disponível, tem-se as seguintes equações:
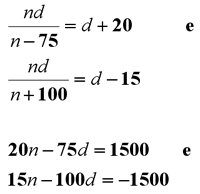
Resolvendo esse sistema de equações, obtém-se que n=300 e d=60.
Vejamos o desafio desta edição, a charada matemática.
Um professor chamou dois alunos inteligentes (vamos chamar de aluno "A" e aluno "B") e deu um papel com um número para cada um. Os números eram inteiros maior que zero. Disse, então, que a soma deste números poderia resultar ou em 1994 ou em 2990. A seguir fez as perguntas:
- Aluno "A", tu sabes qual o número do aluno "B"?
"A" respondeu: Não.
Perguntou para o aluno "B":
- Aluno "B", tu sabes qual o número do aluno "A"?
"B" respondeu: Não.
Voltou para o aluno "A":
- Aluno "A", agora tu sabes qual o número do aluno "B"?
"A" respondeu: Não.
Novamente para o aluno "B":
- Aluno "B", e agora tu sabes qual o número do aluno "A"?
"B" respondeu: Agora eu sei!
Qual o número que "A" recebeu?