CAPÍTULO 4: F90/4 – CONJUNTOS OU VARIÁVEIS INDEXADAS
Até então, em nossos programas, cada posição de memória para armazenar um dado tinha seu nome específico, ou seja, cada variável tinha um único identificador.
Por exemplo:
PI = 3.1416
NOME = “Natália Guimarães Lima”
Neste capítulo introduzimos a idéia que grupos de dados irão compartilhar um único nome em comum e serão diferenciados uns dos outros através de uma numeração que chamaremos de índice. Por exemplo, se tivermos o seguinte grupo de dados contendo 10 nomes de alunos aprovados no vestibular de computação:
Alfredo José da Costa
Aline Lacerda de Menezes
Heber Ribeiro da Cruz
Liliane Lacerda de Menezes
Maria de Fátima Vieira
Mirian Nascimento
Nilce Silva Falcão
Ricardo José Shamá dos Santos
Sérgio Eduardo Lacerda de Meneses
Vania Maria Cabral
podemos identificar este conjunto de dados pelo nome ALUNO e diferenciar:
O 1o. nome, individualizando-o por ALUNO(1);
O 2o. nome, individualizando-o por ALUNO(2);
. . .
O 10o. nome, individualizando-o por ALUNO(10).
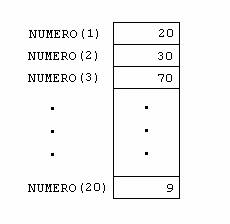
De maneira semelhante, um conjunto de 20 números, pode ser identificado através de um só nome de variável. Por exemplo, o nome NUMERO, onde:
O 1o. número do conjunto seria identificado por NUMERO(1);
O 2o., por NUMERO(2);
. . .
O 20o., por NUMERO(20).
DECLARAÇÃO DE CONJUNTOS
Se estamos trabalhando com variáveis de caracteres, como no caso dos 10 alunos aprovados no curso de computação, a maneira de declarar este conjunto será então:
CHARACTER (LEN=30) :: ALUNOS(10)
Esta declaração nos informa que estamos trabalhando com um conjunto de 10 elementos e que cada elemento possui 30 caracteres de extensão, ou seja:

Se, estamos trabalhando com um conjunto de 20 variáveis numéricas do tipo inteira, cujo nome será NUMERO, declaramos da seguinte maneira:
INTEGER :: NUMERO(20)
então, o seguinte conjunto de números: 20, 30, 70, 201, 55, 67, -82, -33, 27, 80, 100, 13, 14, 16, -1, 27, 33, 2, -3, 9. Seria armazenado na memória da seguinte maneira:
Se, estamos trabalhando com um conjunto de 5 números reais: -25.5, 725.7, -30.0, 0.025, 0.7 e identificamos este conjunto através do nome VETOR, a maneira de declará-lo será então:
REAL :: VETOR(5)
e os números ficarão armazenados da seguinte maneira:

COMO MANUSEAR COM LISTA DE NOMES
O programa a seguir lê uma lista de 50 nomes e apresenta esta mesma lista em ordem inversa a de leitura:
!
!
PROGRAMA QUE INVERTE A ORDEM DE UMA LISTA DE NOMES
!
PROGRAM
ORDEMINVERSA
IMPLICIT NONE
CHARACTER (LEN = 30) :: PESSOA(50)
INTEGER :: INDICE
WRITE (*, *) “APRESENTAÇÃO DE NOMES NA ORDEM
INVERSA A DE LEITURA”
WRITE (*, *) “INFORME OS 50 NOMES, CADA UM
SEGUIDO DE <ENTER>”
WRITE (*, *)
! LEITURA DA LISTA E APRESENTAÇÃO EM ORDEM
DIRETA
DO INDICE = 1, 50, 1
READ (*, *) PESSOA(INDICE)
END DO
! APRESENTAÇÃO DA LISTA EM ORDEM INVERSA
WRITE (*, *) “NOMES NA ORDEM INVERSA: ”
DO INDICE = 50, 1, -1
WRITE (*, *) PESSOA(INDICE)
END DO
STOP
END PROGRAM ORDEMINVERSA
Podemos notar aqui, que a variável INDICE, usada para contar o número de repetições dos DO’s, pode ser usada também para referenciar os diferentes nomes da lista. Exemplo:
Quando INDICE = l estamos lendo um nome para a variável PESSOA(1)
Quando INDICE = 2 estamos lendo um nome para a variável PESSOA(2);
. . .
Quando INDICE = 50 estamos lendo um nome para a variável PESSOA(50).
Em seguida, queremos mostrar a lista na ordem inversa, ou seja, mostrar a lista a partir da variável PESSOA(50), depois PESSOA (49), depois PESSOA (48), ... , depois PESSOA(1).
Desde que o incremento da variável de controle do comando DO pode ser um número negativo, no caso –1, usamos um valor inicial 50 e o final 1. Assim, modificamos o valor da variável de controle do comando DO decrescentemente para obtermos a apresentação das variáveis na ordem desejada.
Exemplo com Variáveis Indexadas
Nosso segundo exemplo mostra um programa que manipula vários tipos de lista. Suponha que a lista é uma tabela do horário dos Professores em uma escola. A tabela será alimentada a partir do teclado. Cada elemento da tabela tem as seguintes informações, relativas a um professor: NOME DO PROFESSOR, HORÁRIO e SALA.
Os dados da tabela são como os que seguem:
NOME DO PROFESSOR HORÁRIO SALA
JOSELUCE 2 BC-105
CAMILO 1 BC-102
ULRICH 4
BC-105
ROBERTO 2 BD-102
FRANCISCO 3 BC-104
ANTÃO 1 CB-101
Nosso objetivo é mostrar esta tabela classificada por horário da seguinte forma:
Professores que dão aula no 1o. horário:
CAMILO
ANTÃO
Professores que dão aula no 2o. horário:
JOSELUCE
ROBERTO
Professores que dão aula no 3o. horário:
FRANCISCO
Professores que dão aula no 4o. horário:
ULRICH
PROGRAM
HORARIOS
IMPLICIT NONE
CHARACTER (LEN = 20) :: PROFESSOR(10)
CHARACTER (LEN = 5) :: SALA(10)
INTEGER :: HORARIO(10), INDICE, HORA
! Leitura dos dados
WRITE (*, *) “Informe o Nome do Professor, o
Horário e a Sala; separados$
& por espaços e terminados
com um <ENTER>”
WRITE (*, *)
DO INDICE = 1,10
READ (*, *) PROFESSOR(INDICE),
HORARIO(INDICE), SALA(INDICE)
END DO
! Se1eciona os professores por horário
DO HORA = 1, 4, 1
WRITE (*, *) “Professores que dão aula no
”, HORA, “o. horário”
DO INDICE = 1, 10, 1
IF (HORARIO(INDICE) .EQ. HORA) THEN
WRITE (*, *) PROFESSOR(INDICE)
END IF
END
DO
END DO
STOP
END PROGRAM HORARIOS
CONJUNTOS BIDIMENSIONAIS
Este caso se aplica a utilização de matrizes, quando precisamos de dois índices para referenciar um elemento do conjunto.
Por exemplo, seja a matriz:

O elemento 18 da matriz está na 3a. linha e na 2a. coluna da matriz. Se, estamos trabalhando com este conjunto em Fortran, e o identificamos pelo nome MATRIZ, devemos declarar, no início do programa, esta variável como:
INTEGER :: MATRIZ(3, 4)
Pois a matriz é de números inteiros e possui 3 linhas 4 colunas. Então o elemento 18 será. referenciado da seguinte maneira:
MATRIZ(3, 2)
Exemplo de programa que lê duas matrizes de mesmas dimensões e realiza a soma entre elas:
PROGRAM
SOMA_MATRIZ
! PROGRAMA QUE SOMA MATRIZES DE DIMENSÕES
2x3
IMPLICIT NONE
INTEGER :: MATA(2,3), MATB(2, 3), MSOMA(2,
3), I, J
WRITE (*, *) “SOMA DE MATRIZES 2x3:”
! LEITURA DAS MATRIZES
WRITE (*, *) “INFORME OS DADOS PARA A
PRIMEIRA MATRIZ: ”
WRITE
(*, *)
READ
(*, *) ((MATA(I, J), J = 1, 3, 1), I = 1, 2, 1)
WRITE (*, *) “INFORME OS
DADOS PARA A SEGUNDA MATRIZ: ”
WRITE
(*, *)
READ
(*, *) ((MATB(I, J), J = 1, 3, 1), I = 1, 2, 1)
! CALCULO DA SOMA
DO I= 1, 2, 1
DO J = 1, 3, 1
MSOMA(I, J) = MATA(I, J) + MATB (I ,J)
END DO
END DO
! IMPRESSÃO DA MATRIZ
WRITE (*, *) “MATRIZ MATA:”
DO I = 1, 2, 1
WRITE(*, *) (MATA(I,J) , J = 1, 3, 1)
END DO
WRITE (*, *)
! IMPRESSÃO DA MATRIZ
WRITE (*, *) “MATRIZ MATB:”
DO I = 1, 2, 1
WRITE (*, *) (MATB(I,J), J = 1, 3, 1)
END DO
WRITE (*, *)
! IMPRESÃO DA MATRIZ SOMA
WRITE (*, *) “MATRIZ SOMA:”
DO I =
1, 2, 1
WRITE (*, *) (MSOMA(I, J), J = 1, 3, 1)
END DO
STOP
END
PROGRAM SOMA_MATRIZ
LEITURA DE DADOS PARA CONJUNTOS DE NUMÉRICOS UNIDIMENSIONAIS
Seja o seguinte conjunto de dados numéricos com apenas dimensão, ou seja, apenas um índice e identificado pela palavra NUMERO:
25.0 75.5 27.9 33.0
A leitura deste conjunto pode ser feita de duas maneiras
a) Cada elemento do conjunto numa linha diferente
REAL :: NUMERO(4)
INTEGER :: I
DO INDICE = 1, 4, 1
READ (*, *) NUMERO(I)
END DO
b) Todos elementos em seqüência numa ou mais linhas de dados separados um elemento do outro por espaço em branco ou uma vírgula.
REAL :: NUMERO(4)
INTEGER :: INDICE
READ (*, *) (NUMERO(INDICE), INDICE = 1, 4, 1)
. . .
LEITURA DE CONJUNTO NUMÉRICO BIDIMENSIONAL (MATRIZ)
A matriz a seguir é uma matriz identificada pela palavra MAT:
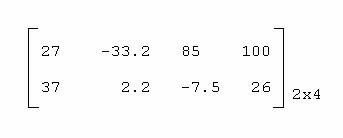
A leitura desta matriz pode ser feita, também, de duas maneiras:
a) Cada elemento numa linha de dados distinta:
INTEGER :: I, J
REAL :: MAT(2, 4)
DO I = 1, 2, 1
DO J = 1, 4, 1
READ (*, *) MAT(I, J)
END DO
END DO
. . .
b) Cada linha da matriz numa ou mais linhas de dados:
INTEGER :: I, J
REAL :: MAT(2, 4)
DO I = 1, 2, 1
READ (*, *) (MAT(I, J), J = 1, 4, 1)
END DO
. . .
c) Todos os elementos da matriz em seqüência num ou mais linhas de dados:
INTEGER :: I, J
REAL :: MAT(2, 4)
READ (*, *) ((MAT(I, J), J = 1, 4,
1), I = 1, 2, 1)
. . .
IMPRESSÃO De CONJUNToS NUMÉRICOS UNIDIMENSIONAIS
De maneira semelhante à leitura, o conjunto de números unidimensionais pode ser impresso de dois modos:
a) Cada elemento numa linha de apresentação:
INTEGER :: INDICE
REAL :: NUMERO(4)
DO INDICE = 1, 4, 1
WRITE (*, *) NUMERO(INDICE)
END DO
. . .
b) Todos os elementos em seqüência numa ou mais linhas de apresentação:
INTEGER :: I
REAL :: NUMERO(4)
WRITE (*, *) (NUMERO(INDICE), INDICE = 1, 4, 1)
. . .
IMPRESÃO DE CONJUNTO DE NÚMEROS BIDIMENSIONAIS (MATRIZES)
Também semelhante à leitura, podemos apresentar este tipo conjunto de 3 maneiras:
a) Cada elemento numa linha de apresentação:
INTEGER :: I, J
REAL :: MAT(2, 4)
DO I = 1, 2, 1
DO J = 1, 4, 1
WRITE (*, *) MAT(I, J)
END DO
END DO
. . .
b) Os elementos de cada linha da matriz numa linha de impressão:
INTEGER :: I, J
REAL :: MAT(3, 4)
DO I = 1, 2
WRITE (*, *) (MAT(I, J), J = 1, 4, 1)
END DO
. . .
c) Todos os elementos da matriz em seqüência, numa ou mais linhas de apresentação:
INTEGER :: I, J
REAL :: MAT(2, 4)
WRITE (*, *) ((MAT(I, J), J = 1, 4, 1), I = 1, 2, 1)
. . .
REFINAMENTO PASSO A PASSO
À medida que nossos problemas Fortran vão aumentando em complexidade, se torna mais difícil sua programação. Por isso, neste ponto, introduzimos uma metodologia de resolução para simplificar a elaboração do programa. Esta metodologia é o refinamento passo a passo.
O refinamento passo a passo consiste em dividir a resolução do problema em etapas e resolver cada etapa separadamente.
Por exemplo, queremos escrever um programa Fortran que classifique (ordene) um conjunto de números qualquer em ordem crescente. Então, nossa solução pode ser dividida em 3 etapas.
1) Ler o conjunto;
2) Ordenar o conjunto;
3) Mostrar o conjunto de números ordenado.
As etapas 1 e 3 podem ser codificadas imediatamente, ou seja:
Etapa 1:
READ (*, *) N
READ (*, *) (NUMERO(I) , I = 1, N, 1)
Etapa 3:
WRITE (*, *) (NUMERO(I), I = l, N, 1)
Neste ponto, notamos que existem 3 variáveis à definir:
N - Quantidade de números do conjunto a ser ordenado;
NUMERO - Variável indexada.unidimensional que conterá os números do conjunto.
I – Variável de controle do comando DO embutida nos comandos READ e WRITE.
Mas deixemos a definição das variáveis para o final da resolução, quando saberemos exatamente quais variáveis devem ser definidas.
Agora vamos a tentar resolver a etapa 2: a ordenação.
Por exemplo, se temos o seguinte conjunto de números ser ordenado crescentemente:
8, 5, -2, 3, 0, -5, -9
Uma das maneiras de ordenar esses números é colocando o maior número na última posição do conjunto, através da troca de posições, quando o maior fosse encontrado. Em Fortran isto é feito da seguinte maneira:
DO INDICE = 1, N - 1
IF (NUMERO(INDICE) .GT. NUMERO(INDICE + 1)
troca posições dos números
END IF
END DO
A troca de posições é feita da seguinte maneira: se (8 .GT. 5) é VERDADE, então coloque o 8 no lugar do 5 e o 5 no lugar do 8.
Se fizermos isto diretamente, vamos perder o valor 5 como é mostrado a seguir:
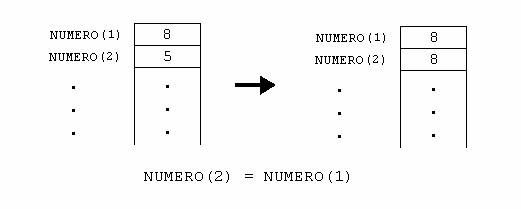
Por isso, vamos utilizar uma variável auxiliar de nome AUX, para realizar a troca:
DO INDICE = 1, N, 1
IF (NUMERO(INDICE) .GT. NUMERO(INDICE + 1)) THEN
AUX = NUMERO(INDICE)
NUMERO(INDICE) = NUMERO(INDICE + 1)
NUMERO(INDICE + 1) = AUX
END IF
END DO
A seqüência na figura a seguir, mostra como isso é realizado:
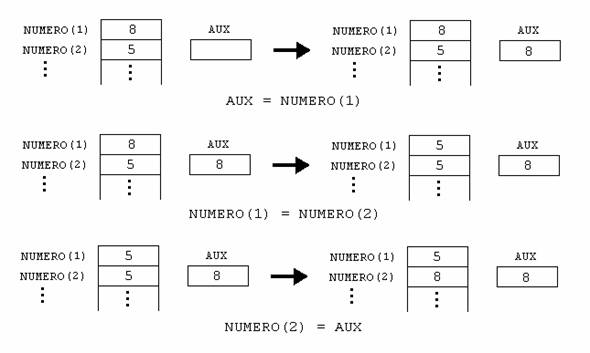
Com esse bloco de comandos, nós conseguimos ordenar apenas o maior valor do conjunto. Como existem N números a serem ordenados, devemos executar este bloco de comandos (N-l) vezes, portanto a ordenação ficará:
DO VEZES = 1, N – 1, 1
DO INDICE = 1, N - 1, 1
IF (NUMERO(INDICE) .GT. NUMERO(INDICE + 1)) THEN
AUX = NUMERO(INDICE)
NUMERO(INDICE) = NUMERO(INDICE + 1)
NUMERO(INDICE + 1) = AUX
END IF
END DO
END DO
E assim resolveremos nosso problema. Agora, vamos juntar tudo para obtermos nosso programa solução.
! ORDENAÇÃO CRESCENTE DE UM CONJUNTO DE 'N' NÚMEROS
PROGRAM ORDENA
! DEFINICÃO DE VARIÁVEIS
INTEGER :: NUMERO(50), INDICE, VEZES, N, AUX
! LEITURA DA QUANTIDADE DE NÚMEROS DO CONJUNTO
WRITE (*, *) “Informe a quantidade de números do conjunto: “
READ (*, *) N
! LEITURA DO CONJUNTO
WRITE (*, *) “Informe os elementos do conjunto: “
READ (*, *) (NUMERO(INDICE), INDICE = 1, N, 1)
! ORDENAÇÃO CRESCENTE COM TROCA DE POSIÇOES
DO VEZES = 1, N - 1, 1
DO INDICE = 1, N - 1, 1
IF (NUMERO(INDICE) .GT. NUMERO(INDICE + 1)) THEN
AUX = NUMERO(INDICE)
NUMERO(INDICE) = NUMERO(INDICE + 1)
NUMERO(INDICE + 1) = AUX
END IF
END DO
END DO
! IMPRESSÃO DO CONJUNTO ORDENADO
WRITE (*, *) “Conjunto de números ordenados: “
WRITE (*, *) (NUMERO(INDICE), INDICE = 1, N, 1)
STOP
END PROGRAM
ORDENA
Notar que a especificação INTEGER :: NUMERO(50) significa que este programa pode ordenar um conjunto número inteiros até 50 elementos.
LISTA DE EXERCÍCIOS
1) Fazer um programa Fortran que ordene alfabeticamente uma lista contendo N nomes. Considerar que 1 £ N £ 100.
2) Fazer um programa Fortran que determine o conjunto união entre dois conjuntos de números dados. Por exemplo:
A = {25, -5, 83, 27, -30, 90, 13}
B = { -5, 0, 27, -30, 90, 13}
AÈB = {25, -5, 83, 27, -30, 0, 90, 13}
3) Fazer um programa Fortran que imprima o maior elemento e o menor elemento de uma matriz qualquer de dimensão MxN, acompanhados de suas posições (índices de linha e coluna). Considerar que 1 £ M £10 e 1 £ N £ 12. Exemplo:
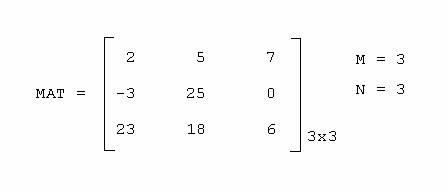
Mensagens:
O maior elemento é 25 que está na linha 2 e coluna 2.
O menor elemento é -3 que está na linha 2 e coluna 1.
4) Fazer um programa Fortran que, dada a seguinte tabela de distâncias em quilômetros entre as cidades A, B, C e D, calcular e imprimir uma tabela contendo o tempo gasto em horas para ir de uma cidade a outra, supondo que você dirige a uma velocidade constante de 60 Km/h
|
|
A |
B |
C |
D |
|
A |
0 |
30 |
90 |
120 |
|
B |
30 |
0 |
60 |
150 |
|
C |
90 |
60 |
0 |
200 |
|
D |
120 |
150 |
200 |
0 |