CAPÍTULO 5: F90/5 – SUBPROGRAMAS

Neste subconjunto introduziremos a idéia de subprogramas. A necessidade do subprograma surgiu na medida que os programas foram tornando-se maiores e mais complexos. Notou-se que um programa muito grande poderia ser dividido em vários subprogramas gerenciados por um programa principal, e que isso facilitava a compreensão do mesmo. Verificou-se também, que parte da solução de um problema poderia ser utilizada na resolução de muitos problemas diferentes e por isso, aquela parte da solução, sendo um subprograma, daria a facilidade de ser usado em vários programas com objetivos diferentes. E mais, os subprogramas poderiam ser feitos por pessoas diferentes e ao mesmo tempo, diminuindo assim o tempo de programação.

Por exemplo, um subprograma que determina a inversa uma matriz pode ser usada:

· na matemática, para resolver sistemas de equações lineares;

· na engenharia civil, no cálculo estrutural;

· na engenharia elétrica, para calcular admitâncias de linhas de transmissão.

Tipos de Subprogramas

Subprogramas Função Predefinida (Função Embutida ou Intrínseca)

São subprogramas que realizam funções largamente usadas nos nossos cálculos, tais como:

SIN(X)

COS(X)

ALOG(X)

IFIX(X)

FLOAT(X)

MOD(I, J)

SQRT(X)

etc.

Estas funções são fornecidas pelo fabricante do compilador e por isso têm o nome de pré-definidas. Uma maneira de utilizá-las é através do comando de atribuição:

nome da variável = função(argumentos)

Por exemplo, o resto da divisão inteira do número 17 pelo número 5 é dada por:

- os argumentos da função é 17 e 5;

- a função pré-definida é MOD;

- o nome da variável é RESTO;

Então a chamada da função dentro do programa será:

RESTO = MOD(17, 5)

Outra maneira, é utilizar a função no lugar onde você utilizaria uma variável, ou seja, como operando de uma expressão. Por exemplo:

IF (MOD(VALOR, 2) .EQ. 0) THEN

Ou ainda, podemos utilizar a função como um elemento a ser mostrado num comando de saída:

WRITE (*, *) “VALOR DA FUNÇÃO = ”, &

&MOD(INTEIRO1, INTEIRO2)

Subprograma Função (FUNCTION)

O subprograma função, ou simplesmente função, é semelhante ao subprograma função pré-definida, com a diferença que:

- A função pré-definida é desenvolvida pelo fabricante do compilador para produzir o resultado de alguma função de uso muito freqüente;

- A função é feita pelo programador para produzir um valor qualquer a partir da execução de uma computação do seu interesse.

A chamada de uma função pode ser feita de dentro do programa principal ou de dentro de outro subprograma, e é semelhante à chamada da função pré-definida. Uma forma de se chamar uma função é:

nome-de-variável = nome-da-função(argumentos-de-entrada)

Onde:

nome-de-variável - é a variável onde vamos guardar o valor produzido e devolvido pela função.

nome-da-função - nome dado à função que o módulo de chamada (programa principal ou subprograma) vai utilizar.

argumentos-de-entrada - lista de valores (constantes, variáveis e/ou expressões) com os quais a função vai trabalhar para determinar e devolver o resultado.

Estrutura de um Subprograma função

A estrutura de um subprograma função é a seguinte:

FUNCTION nome_da_função (parâmetros_de_entrada)

Declarações de parâmetros e variáveis

Comandos FORTRAN

RETURN

END FUNCTION nome_da_função

FUNCTION - significa que este subprograma é uma função.

nome_da_função - deve ser declarado com o tipo (INTEGER, REAL, etc.) do retorno da função. Funciona como uma pseudo-variável que deverá conter o resultado da função.

parâmetros_de_entrada - lista de variáveis que deverão receber os argumentos de chamada da função – todas devem ser declaradas.

Exemplo:

Suponha um programa para determinar qual foi a maior temperatura alcançada durante o mês de Maio, aqui em C. Grande. O programa deve ler a quantidade de medidas de temperaturas tomadas neste mês e as respectivas temperaturas. Em seguida, chamar um subprograma função para determinar o maior elemento do conjunto de temperaturas e finalmente mostrar o maior elemento.

Então, nosso programa seria:

!

! Encontra a maior de um número informado de temperaturas

!

! Programa principal

PROGRAM maior_temperatura

IMPLICIT NONE

! Definição de variáveis

INTEGER :: indice, numero_temperaturas

REAL :: temperaturas(20), maior

! Apresentação da finalidade do programa

WRITE(*, *) "Mostra o maior valor de N temperaturas:"

WRITE(*, *)

! Leitura do número de temperaturas

WRITE (*, *) "Informe o número de temperaturas (máximo 20):"

READ (*,*) numero_temperaturas

! Leitura das temperaturas

WRITE (*, *)"Informe as", numero_temperaturas, "temperaturas"

READ (*, *) (temperaturas(indice), &

&indice = 1, numero_temperaturas, 1)

! Chamada da função maior e impressão da maior temperatura

WRITE(*, *)

WRITE(*, *) "Temperatura Máxima =", &

&maior(numero_temperaturas, temperaturas)

STOP

END PROGRAM maior_temperatura

!

! Função que acha o maior de um conjunto de números reais

!

! Subprograma função

FUNCTION maior(tamanho, conjunto)

IMPLICIT NONE

! Declaração dos parâmetros, declaração do retorno da função

! e declarações das variáveis da função

INTEGER :: tamanho, indice

REAL :: maior, conjunto(tamanho)

! define o primeiro como maior

maior = conjunto(1)

! procura o maior

DO indice = 2, tamanho, 1

IF(conjunto(indice) .GT. maior) THEN

maior = conjunto(indice)

END IF

END DO

! encerramento da função com retorno do resultado

RETURN

END FUNCTION maior

Neste exemplo, a função começa a ser executada quando é chamada pelo programa principal através do comando:

maior(numero_temperaturas, temperaturas)

Onde:

- maior - nome da função

- numero_temperaturas e temperaturas - argumentos de entrada

Observe que ao chegar no RETURN, nome da função, maior, possui o maior elemento do conjunto, que é exatamente o valor numérico que desejamos obter deste subprograma função.

A correspondência entre os argumentos do programa principal com os parâmetros da função, é feita da seguinte maneira:

- O primeiro argumento de chamada da função, numero_temperaturas, corresponde ao primeiro parâmetro de definição da função, tamanho.

- O segundo argumento de chamada da função, temperaturas, corresponde ao segundo parâmetro de definição da função, conjunto.

Os argumentos (constantes ou variáveis) devem ser dados de mesmo tipo que seus parâmetros correspondentes. Então, o conteúdo de numero_temperaturas do programa principal é transferido para a variável tamanho da função. Da mesma maneira, o conteúdo da variável indexada temperaturas do programa principal é transferida para a variável indexada conjunto da função e quando a função está procurando o maior elemento de conjunto, ele na realidade está procurando a temperatura máxima do conjunto temperaturas.

Subprograma Sub-rotina (SUBROUTINE)

O subprograma sub-rotina é semelhante ao subprograma função com algumas diferenças que iremos descobrindo no decorrer do texto, A primeira diferença é que a sub-rotina pode devolver ao programa principal (ou a outro subprograma) mais de um valor, ao contrário da função que é só capaz de devolver apenas um valor quando é chamada pelo programa principal (ou por outro subprograma).

A chamada de um subprograma sub-rotina dentro de um programa principal (ou de outro subprograma) é feita da seguinte maneira:

CALL nome_da_sub-rotina(argumentos_de_entrada, argumentos_de_saída, argumentos_de_entrada_e_saida)

Onde:

- CALL - é uma palavra reservada do Fortran que determina a chamada de uma sub-rotina.

- nome_da_sub-rotina - nome pela qual será identificada esta sub-rotina. Deve ter até 31 caracteres, sendo o primeiro obrigatoriamente uma letra, e pode ser composto de letras (o sublinha é considerado uma letra) e dígitos.

- argumentos_de_entrada - são todos os valores (constantes, variáveis e/ou expressões) que a sub-rotina vai utilizar para computar os conteúdos dos argumentos de saída.

- argumentos_de_saída - são as variáveis que vão conter os valores utilizados na computação pela sub-rotina e que serão devolvidos ao programa principal (ou para outro subprograma) para posterior utilização.

- argumentos_de_entrada_e_saída - são as variáveis que a sub-rotina vai utilizar, modificando seu conteúdo para conter os valores computados pela própria sub-rotina e que serão devolvidos ao programa principal (ou a outro subprograma) para posterior utilização.

Estrutura de um Subprograma Sub-rotina

SUBROUTINE nome_da_sub-rotina(parâmetros_de_entrada,

parâmetros_de_saída,

parâmetros_de_entrada_e_saída)

Declarações deparâmetros e variáveis

Comandos Fortran

RETURN

END SUBROUTINE nome_da_sub-rotina

Onde:

- SUBROUTINE - significa que o subprograma é do tipo sub-rotina.

- nome_da_sub-rotina - nome pelo qual é identificada esta sub-rotina.

- parâmetros_de_entrada - nomes de variáveis com a qual a sub-rotina vai trabalhar para determinar os parâmetros de saída.

- parâmetros_de_saída - nomes de variáveis que guardarão os resultados calculados pela sub-rotina.

- parâmetros_de_entrada_e_saída - nomes de variáveis que receberão valores que serão modificados e devolvidos pela sub-rotina.

- RETURN - comando Fortran que devolve ao programa principal (ou para outro subprograma) o controle de execução que neste ponto estava com a sub-rotina.

Por Exemplo, suponha um programa para determinar a matriz transposta de uma matriz lida da entrada padrão. O programa deve apenas:

- ler as dimensões da matriz

- ler a matriz

- chamar uma sub-rotina para determinar a matriz transposta

- imprimir a matriz transposta.

Então o programa seria:

!

! Programa para calcular a matriz_transposta de uma matriz real de no máximo

! 4 linhas e 5 colunas

!

! Programa principal

PROGRAM calcula_matriz_transposta

IMPLICIT NONE

! Declaração das variáveis

INTEGER :: i, j, num_lin, num_col, num_lin_transp, num_col_transp

REAL :: matriz(4, 5), matriz_transposta(5, 4)

! Leitura do numero de linhas e colunas da matriz

WRITE (*, *) "calcula e mostra a transposta de uma matriz lida:"

WRITE (*, *)

WRITE (*, *) "Informe o número de linhas (máximo 4) e"

WRITE (*, *) "e o número de colunas (máximo 5) da matriz:"

READ (*, *) num_lin, num_col

WRITE (*, *) "Informe os elementos da matriz:"

READ (*, *) ((matriz(i, j), j = 1, num_col, 1), i = 1, num_lin, 1)

! Chamada da sub-rotina

CALL transposta(num_lin, num_col, matriz, num_lin_transp, num_col_transp,&

& matriz_transposta)

! Apresentação da matriz lida

WRITE (*, *)

WRITE(*, *) "Matriz lida:"

DO i = 1, num_lin, 1

WRITE(*, *) (matriz(i, j), j = 1, num_col, 1)

END DO

! Apresentação da matriz transposta

WRITE (*, *)

WRITE(*, *) "Matriz transposta:"

DO i = 1, num_lin_transp, 1

WRITE(*, *) (matriz_transposta(i, j), j = 1, num_col_transp, 1)

END DO

STOP

END PROGRAM calcula_matriz_transposta

!

! Sub-rotina que calcula a transposta de uma matriz real

!

! Subprograma sub-rotina

SUBROUTINE transposta(nLin, nCol, mat, nLin_trans, nCol_trans, mat_trans)

IMPLICIT NONE

! Declaração dos parâmetros, declaração do retorno da função

! e declarações das variáveis da função

INTEGER :: nLin, nCol, nLin_trans, nCol_trans, i, j

REAL :: mat (4, 5), mat_trans(5, 4)

! Geração da transposta

DO i = 1, nLin, 1

DO j = 1, nCol, 1

mat_trans(j, i) = mat(i, j)

END DO

END DO

! Geração do número linhas e colunas da transposta

nLin_trans = nCol

nCol_trans = nLin

! Encerramento da sub-rotina

RETURN

END SUBROUTINE transposta

Neste exemplo, a sub-rotina começa a ser executada quando é chamada pelo programa principal através do comando:

CALL transposta(num_lin, num_col, matriz, num_lin_transp, num_col_transp,$

& matriz_transposta)

Observe que ao chegar no RETURN em nLin_trans temos a dimensão de coluna da matriz transposta, em nCol_trans temos a dimensão de coluna da matriz transposta e em mat_trans temos a transposta da matriz mat.

A correspondência entre os argumentos de entrada e saída do programa principal com os parâmetros de entrada e saída da sub-rotina é feita da seguinte maneira:

- Na chamada, ou seja, na execução do comando CALL:

O conteúdo de num_lin é transferido para nLin;

O conteúdo de num_col é transferido para nCol;

O conteúdo da variável indexada matriz é transferido para a variável indexada mat.

- No retorno, ou seja, na execução do comando RETURN:

O conteúdo de nLin_trans é transferido para num_lin_transp;

O conteúdo de nCol_trans é transferido para num_col_transp;

O conteúdo da variável indexada mat_trans é transferido para a variável indexada matriz_transposta.

Como Chamar uma Sub-rotina numa Biblioteca

Quando queremos utilizar uma sub-rotina que já exista numa biblioteca (coleção de subprogramas), precisamos de informações adicionais para sabermos exatamente quais os parâmetros ela usa e qual é o tipo de cada parâmetro. Para isso, devemos utilizar uma documentação que pode ser o manual do usuário da biblioteca ou alguma opção de ajuda em software que a mesma possua.

Exemplo de Função

Programar uma função que converte um número binário no seu equivalente na base decimal.

Para converter um número binário em decimal fazemos da seguinte maneira:

(100011)₂ = 1 x 2⁵ + 0 x 2⁴ + 0 x 2³ + 0 x 2² + 1 x 2¹ + 1 x 2⁰

= 32 + 0 + 0 + 0 + 2 + 1

= (35)₁₀

O algoritmo que utilizaremos para conversão será:

d₀ = b₀

d₁ = 2 x d₀ + b₁

. . .

d_n = 2 x d _(n-1) + b_n

Se o número é (100011)₂, então n = 5 e b₀ = 1, b₁ = 0, b₂ = 0, b₃ = 0, b₄ = 1 e b₅ = 1.

Usando o número acima e aplicando o algoritmo obtemos:

d0 = 1

d1 = 2 x 1 + 0 = 2

d2 = 2 x 2 + 0 = 4

d3 = 2 x 4 + 0 = 8

d4 = 2 x 8 + 1 = 17

d5 = 2 x 17 + 1 = 35

Então o subprograma função utilizando este algoritmo será:

!

! Programa que lê um número binário e o converte para decimal

!

! Programa principal

PROGRAM binario_para_decimal

IMPLICIT NONE

! Declaração das variáveis e do tipo da função

INTEGER :: binario, bindec

! Apresentação da finalidade do programa

WRITE (*, *) "Converte um inteiro binário lido para decimal:"

WRITE (*, *)

! Leitura do valor binário para um inteiro decimal

WRITE (*, *) "Informe o número binário (máximo 10 dígitos):"

READ (*, *) binario

! Chama a função que converte de binário para inteiro e

! mostra o resultado da conversão

WRITE (*, *)

WRITE (*, *) "Valor convertido para decimal:", bindec(binario)

STOP

END PROGRAM binario_para_decimal

!

! Função que converte um inteiro binário (com 0's e 1's) para decimal

!

! Subprograma função

FUNCTION bindec(binario)

IMPLICIT NONE

! Declaração do retorno da função, do parâmetro de entrada e

! das variáveis da função

INTEGER :: bindec, binario, digito, vezes, potencia_de_2

! Inicializa para o somatório

bindec = 0

! Inicialização da potência de 2 com 2**0

potencia_de_2 = 1

DO vezes = 1, 10, 1

! Separa um dígito binário

digito = MOD(binario, 2)

! Soma o valor da potência da posição do dígito no decimal

bindec = bindec + digito * potencia_de_2

! Calcula a potência da posição do próximo dígito

potencia_de_2 = potencia_de_2 * 2

! Elimina o dígito da potência já somada

binario = binario / 10

END DO

! Encerra a função retornando o valor final de bindec

RETURN

END FUNCTION bindec

Exemplo de Sub-rotina

Programar uma sub-rotina que converta um número inteiro positivo na base decimal para. seu equivalente na base binária.

Para converter um número decimal em binário dividimos este número sucessivamente por 2 até obtermos resto e quociente iguais a zero. O resto das divisões de cada uma das divisões sucessivas na ordem inversa é o resultado que procuramos.

Exemplo:

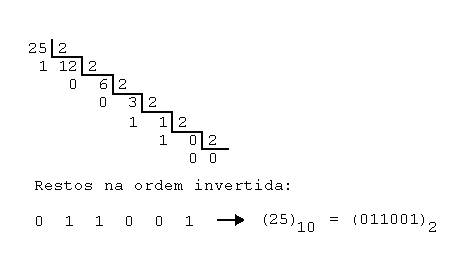
Parâmetro de entrada da Sub-rotina:

- Número em decimal

Parâmetros de saída:

- Vetor contendo o respectivo número em binário

- Dimensão do vetor

O programa com a sub-rotina ficará então:

!

! Programa que lê um número decimal e o converte para binário

!

! Programa principal

PROGRAM decimal_para_binario

IMPLICIT NONE

! Declaração das variáveis e do tipo da função

INTEGER :: decimal, binario

! Apresentação da finalidade do programa

WRITE (*, *) "Converte um inteiro decimal lido para binário:"

WRITE (*, *)

! Leitura do valor binario para um inteiro decimal

WRITE (*, *) "Informe o número decimal (máximo 10 digitos):"

READ (*, *) decimal

! Chama a sub-rotina que converte de decimal para binário

CALL decbin(decimal, binario);

! Mostra o resultado da conversão

WRITE (*, *)

WRITE (*, *) "Valor convertido para binário:", binario

STOP

END PROGRAM decimal_para_binario

!

! Sub-rotina que converte um inteiro binário (com 0's e 1's) para decimal

!

! Subprograma sub-rotina

SUBROUTINE decbin(decimal, binario)

IMPLICIT NONE

! Declaração de parâmetros e variáveis

INTEGER :: decimal, binario, dividendo, quociente, expoente_de_10

! Conversão de decimal para binário dígito a dígito

dividendo = decimal

quociente = dividendo / 2

expoente_de_10 = 0

binario = 0

DO WHILE (quociente .NE. 0)

binario = binario + 10**expoente_de_10 * MOD(dividendo, 2)

dividendo = quociente

quociente = dividendo / 2

expoente_de_10 = expoente_de_10 + 1

END DO

binario = binario + 10**expoente_de_10 * MOD(dividendo, 2)

! Encerramento da sub-rotina

RETURN

END SUBROUTINE decbin

Mais exemplos

1) Programa para somar matrizes inteiras com dimensões máximas 10x10:

!

! Programa para somar matrizes inteiras com dimensões máximas 10x10

!

! Programa principal

PROGRAM soma_matrizes

IMPLICIT NONE

! Declarações das variáveis do programa

INTEGER :: mat1(10, 10), mat2(10, 10), matS(10, 10), lin, col

INTEGER :: indl, indc

! Apresentação da finalidade do programa

WRITE (*, *) "Programa para somar matrizes inteiras com dimensões&

& máximas 10x10:"

WRITE (*, *)

! Leitura das dimensões da matriz

WRITE(*,*)"Informe o numero de linhas e colunas das matrizes:"

READ(*,*)lin, col

! Leitura dos dados da primeira matriz

WRITE(*,*)"Informe os dados para a primeira matriz a somar:"

CALL lemat(mat1, lin, col)

! Leitura dos dados da segunda matriz

WRITE(*,*)"Informe os dados para a segunda matriz a somar:"

CALL lemat(mat2, lin, col)

! Soma das matrizes

DO indl = 1, lin, 1

DO indc = 1, col, 1

matS(indl, indc) = mat1(indl, indc) + mat2(indl, indc)

END DO

END DO

! Impressão da primeira matriz

WRITE(*,*) "Primeira Matriz:"

CALL impmat(mat1, lin, col)

! Impressão da segunda matriz

WRITE(*,*) "Segunda Matriz:"

CALL impmat(mat2, lin, col)

! Impressão da matriz soma

WRITE(*,*) "Matriz Soma:"

CALL impmat(matS, lin, col)

STOP

END PROGRAM soma_matrizes

!

! Sub-rotina que lê uma matriz

!

! Subprograma sub-rotina

SUBROUTINE lemat(mat, lin, col)

IMPLICIT NONE

! Declaração dos parâmetros e das variáveis da sub-rotina

INTEGER :: mat(10, 10), lin, col, l, c

! Leitura dos elementos da matriz

DO l = 1, lin, 1

DO c = 1, col, 1

READ(*,*)mat(l, c)

END DO

END DO

! Encerramento da sub-rotina

RETURN

END SUBROUTINE lemat

!

! Sub-rotina que imprime uma matriz

!

! Subprograma sub-rotina

SUBROUTINE impmat(mat, lin, col)

IMPLICIT NONE

INTEGER :: mat(10, 10), lin, col, l, c

! Impressão dos elementos da matriz

DO l = 1, lin, 1

WRITE(*,*) (mat(l, c), c = 1, col, 1)

END DO

! Encerramento da sub-rotina

RETURN

END SUBROUTINE impmat

2) Programa para calcular a soma dos fatoriais de dois números inteiros usando uma função:

!

! Programa que calcula a soma dos fatoriais de dois números

!

! Programa principal

PROGRAM soma_fatoriais

IMPLICIT NONE

! Declaração das variáveis do programa

INTEGER :: valor1, valor2, fatorial

! Apresentação

WRITE (*, *) "Mostra a soma do fatorial de dois números:"

WRITE (*, *)

! Leitura dos dois inteiros

WRITE (*, *) "Informe os dois inteiros:"

READ (*, *) valor1, valor2

WRITE (*, *)

! Chamada dupla da função fatorial e apresentação da soma

WRITE (*, *) "A soma dos fatoriais dos dois números eh",&

& fatorial(valor1) + fatorial(valor2)

STOP

END PROGRAM soma_fatoriais

!

! Função que calcula o fatorial de um número

!

FUNCTION fatorial(numero)

IMPLICIT NONE

! Declarações do retorno, do parâmetro e variável da função

INTEGER :: numero, fatorial, fator

! Cálculo do fatorial

fatorial = 1

DO fator = numero, 1, -1

fatorial = fatorial * fator

END DO

! Encerramento da função com retorno do resultado pelo nome

! da função

RETURN

END FUNCTION fatorial

3) Programa para ler dois inteiros fazendo uma comparação de valores entre eles, utilizando uma função comparadora:

!

! Programa que compara dois inteiros e informa através de uma mensagem

! a relação entre eles

!

! Programa principal

PROGRAM comparaInteiros

IMPLICIT NONE

! Declaração das variáveis do programa e do retorno da função

INTEGER :: numero1, numero2, retorno, comparaInt

! Apresentação da finalidade do programa

WRITE (*,*) "Compara dois inteiros e informa a relação entre eles:"

WRITE (*,*)

! Leitura dos valores a serem comparados

WRITE (*,*) "Informe os 2 numeros inteiros para serem comparados: "

READ (*,*) numero1, numero2

! Chama a função comparadora e armazena o resultado da comparação

retorno = comparaInt(numero1, numero2)

! Emite mensagem de acordo com o resultado armazenado

IF (retorno .EQ. -1) THEN

WRITE (*,*) "O primeiro ", numero1, " é menor que o segundo ", numero2

ELSE IF (retorno .EQ. 0) THEN

WRITE (*,*) "O primeiro ", numero1, " é igual ao segundo ", numero2

ELSE

WRITE (*,*) "O primeiro ", numero1, " é maior que o segundo ", numero2

END IF

! Encerra o programa

STOP

END PROGRAM comparaInteiros

!

! Funçao para comparar numeros inteiros

!

! Sub-programa função

FUNCTION comparaInt (inteiro1, inteiro2)

! Declarações do nome e dos parâmetros da função

IMPLICIT NONE

INTEGER :: comparaInt, inteiro1, inteiro2

! Comparação dos valores recebidos

IF (inteiro1 .LT. inteiro2) THEN

comparaInt = -1

ELSE IF (inteiro1 .EQ. inteiro2) THEN

comparaInt = 0

ELSE

comparaInt = 1

END IF

! Encerra a função retornando o resultado no nome da função

RETURN

END FUNCTION comparaInt

EXERCÍCIOS:

1) Fazer um programa que lê uma lista com as letras de teu nome. Em seguida verifica se as letras ‘A’ e ‘B’ estão contidos na lista. Esta verificação é feita por uma função CONTIDO_EM(letra, lista) a ser desenvolvida.

2) Faça uma função POT(X,N) que calcula o expoente xⁿ, para um real x e um inteiro n.

3) Sabendo que o desenvolvimento em série de sen(x) é 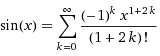faça uma função SENO(x,k) que calcula os k primeiros elementos desta série dados um k e um x. Use POT(x,n) da questão anterior e a função FATORIAL(k).

Em seguida cria um programa que compara os resultados da função SIN(x) do FORTRAN com SENO(x,3) e SENO(X,5).

4) Faça um programa que leia um conjunto (Vetor) de 10 Notas. Calcule e imprima o desvio padrão

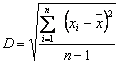
O programa deve conter subprogramas para as seguintes tarefas:

- Ler vetor

- Imprimir Vetor

- Calcular Valor Médio

- Calcular desvio padrão

5) Faça um programa que receba duas datas, uma como três inteiros DIA, MÊS e ANO e outra como uma cadeia “dd/mm/aaaa” e verifica qual é anterior. Para tal, usa duas funções que convertem os formatos em um inteiro da forma aaammdd e verifica qual é menor.

. Exemplo: para comparar DIA=15 MÊS=10 e ANO=2012 com “21/09/2012” eles são convertidos em 20121015 e 20120921 respectivamente para se verificar que a segunda data é anterior à primeira. Para converter os dígitos da cadeia “dd/mm/aaaa” use a seguinte função, que converte um dígito, p.ex. “2” em um número, no exemplo, 2012:

function dig_to_num (d)

integer dig_to_num

character (len=1) d

if (d .eq. "1") then

dig_to_num = 1

end if

if (d .eq. "2") then

dig_to_num = 2

end if

if (d .eq. "3") then

dig_to_num = 3

end if

if (d .eq. "4") then

dig_to_num = 4

end if

if (d .eq. "5") then

dig_to_num = 5

end if

if (d .eq. "6") then

dig_to_num = 6

end if

if (d .eq. "7") then

dig_to_num = 7

end if

if (d .eq. "8") then

dig_to_num = 8

end if

if (d .eq. "9") then

dig_to_num = 9

end if

if (d .eq. "0") then

dig_to_num = 0

end if

return

end function dig_to_num

6)