Representação de Grafos
A representação gráfica que utilizamos é necessária para a rápida compreensão e utilização na definição dos conceitos básicos da teoria dos gráficos. De fato, na maioria das situações práticas, utilizamos esse tipo de representação. Esta representação gráfica, entratento, não é adequada para representar internamente (em um computador) dados sobre a estrutura de um grafo. É necessário uma representação que o computador possa entender.
Existem várias formas de representar um grafo ![]() . Variações
em termos de tamanho do grafo e de sua complexidade, propiciaram diversas
formas de representação de um grafo. As mais conhecidas são:
. Variações
em termos de tamanho do grafo e de sua complexidade, propiciaram diversas
formas de representação de um grafo. As mais conhecidas são:
A representação com listas de adjacência é mais utilizada porque provê
uma forma compacta de representar grafos esparsos , isto é, grafos
onde ![]() é bem menos do que
é bem menos do que ![]() .
.
A representação com matriz de adjacência é indicada no caso de grafos
densos, onde ![]() é perto de
é perto de ![]() .
.
A representação com listas de adjacência de um grafo ![]() consiste de um
array
consiste de um
array ![]() de
de ![]() listas, um para cada vértice de
listas, um para cada vértice de ![]() . Para cada
. Para cada ![]() ,
a lista de adjacência
,
a lista de adjacência ![]() contém um ponteiro para todos os vértices
contém um ponteiro para todos os vértices ![]() ,
onde existe um arco
,
onde existe um arco ![]() . Logo,
. Logo, ![]() consiste de todos os vértices
de
consiste de todos os vértices
de ![]() que são adjacentes a
que são adjacentes a ![]() . Esses vértices são armazenados em ordem
arbitrária.
. Esses vértices são armazenados em ordem
arbitrária.
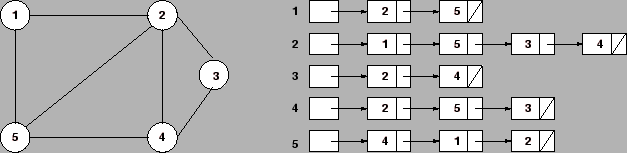
A figura abaixo mostra um grafo não dirigido e sua representação com listas de adjacência.
Se ![]() é um grafo dirigido, a soma dos tamanhos de todas as listas de
adjacências é
é um grafo dirigido, a soma dos tamanhos de todas as listas de
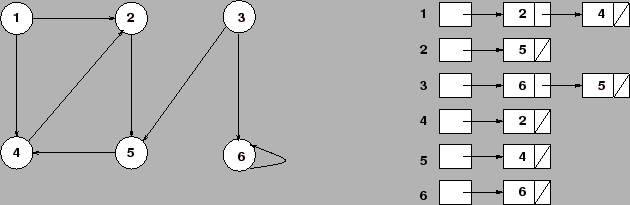
adjacências é ![]() . A figura abaixo mostra um grafo dirigido e sua representação
com listas de adjacência.
. A figura abaixo mostra um grafo dirigido e sua representação
com listas de adjacência.
Em ambos os casos, grafos dirigidos ou não, a representação com listas de
adjacÊncia possui uma propriedade desejável que indica que a quantidade de
memória requerida é
![]() .
.
As listas de adjacência também pode ser utilizadas no caso de grafos ponderados e outras variantes de grafos.
A maior desvantagem desse método de representação é a de não possuir uma
forma eficiente de dizer se um determinado arco ![]() está presente no
grafo.
está presente no
grafo.
A representação por matriz de adjacência de um grafo ![]() requer
que os vértices sejam arbitrariamente numerados de
requer
que os vértices sejam arbitrariamente numerados de
![]() . A matriz
de adjacência de um grafo de uma matriz
. A matriz
de adjacência de um grafo de uma matriz ![]() , de ordem
, de ordem
![]() , onde
, onde
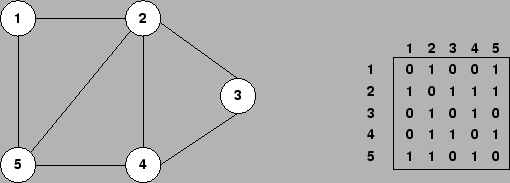
A figura abaixo mostra um grafo não dirigido e sua representação com matriz de
adjacência. Esse tipo de representação requer ![]() de memória,
independentemente do número de arcos do grafo.
de memória,
independentemente do número de arcos do grafo.
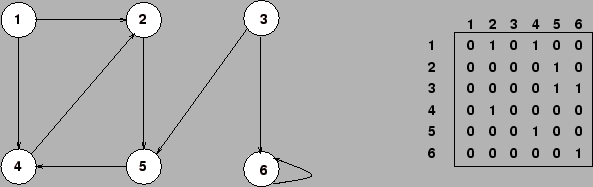
Da mesma forma, a matriz de adjacência pode ser usada para representar grafos dirigidos.
Como na representação com listas de adjacência, a matriz de adjacência pode
ser usada para representar grafos ponderados. Em vez de usar ![]() para indicar a
presença do arco, utiliza-se o peso do arco.
para indicar a
presença do arco, utiliza-se o peso do arco.
Embora a representação com lista de adjacência seja pelo menos tão eficiente quanto a representação com matriz de adjacência, a simplicidade de uma matriz de adjacência a torna preferível no caso de grafos pequenos. No caso de grafos não ponderados, a representação com matriz de adjacência tem a vantagem de requerer apenas um bit por entrada.
A representação por matriz de adjacência de um grafo ![]() é uma matriz
de dimensões
é uma matriz
de dimensões ![]() , na qual cada linha corresponde a um vértice e cada
coluna a uma aresta.
, na qual cada linha corresponde a um vértice e cada
coluna a uma aresta.
A matriz de incidência de um grafo (não dirigido), ![]() ,
de ordem
,
de ordem
![]() , onde
, onde
![]() .
.
![]() .
.
No caso de um grafo dirigido e sem laço, a matriz de incidência de um grafo, ![]() ,
de ordem
,
de ordem
![]() , onde
, onde
![]() e
e ![]() .
.
![]() .
.