Análise e Técnicas de Algoritmos
Período 2003.2
Relação de Recorrência
- A análise de um algoritmo recursivo requer a
resolução de uma recorrência.
- Uma recorrência é um algoritmo recursivo que calcula
o valor de uma função em um ponto dado.
- Uma recorrência define T(n) em termos de T(n-1), T(n-2),
etc.
Exemplo 1:
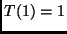 e
e
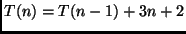 , para
, para 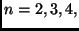 etc.
etc.
Para valores pequenos de 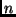 , temos os seguintes valores de
T(n):
, temos os seguintes valores de
T(n):
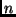 |
1 |
2 |
3 |
4 |
5 |
6 |
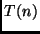 |
1 |
9 |
20 |
34 |
51 |
71 |
Exemplo 2:
Considere a figura abaixo:
Quantos pedaços obtemos com 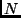 cortes na pizza?
cortes na pizza?
É possível observar que o 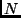 -ésimo corte
cria
-ésimo corte
cria 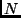 novas fatias. Logo, o número total de
fatias obtido com
novas fatias. Logo, o número total de
fatias obtido com 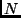 cortes, denotado por
cortes, denotado por 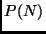 ,
é dado pela seguinte relação de recorrência:
,
é dado pela seguinte relação de recorrência:
Como proceder para derivar uma relação de
recorrência para a análise do tempo de
execução de um algoritmo:
- Determinar qual o tamanho
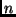 do problema.
do problema.
- Verificar que valor de
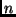 é usado como base da
recursão. Em geral é um valor único (
é usado como base da
recursão. Em geral é um valor único (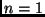 , por exemplo), mas pode ser valores múltiplos.
Vamos considerar esse valor como
, por exemplo), mas pode ser valores múltiplos.
Vamos considerar esse valor como 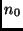 .
.
- Determinar
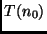 . Pode-se usar uma constante
. Pode-se usar uma constante 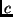 , mas, em muitos, casos um número específico
é necessário.
, mas, em muitos, casos um número específico
é necessário.
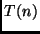 é definido como uma soma de
várias ocorrências de
é definido como uma soma de
várias ocorrências de 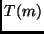 (chamadas
recursivas), mais a soma de outras instruções efetuadas.
Em geral, as chamadas recursivas estão relacionadas com
(chamadas
recursivas), mais a soma de outras instruções efetuadas.
Em geral, as chamadas recursivas estão relacionadas com 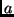 subproblemas do mesmo tamanho
subproblemas do mesmo tamanho 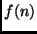 , definindo um
termo
, definindo um
termo 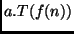 na relação de
recorrência.
na relação de
recorrência.
Logo, a relação de recorrência é definida
como:
Exemplo 1: O problema do corte das pizzas
No problema do corte das pizzas, a relação de
recorrência 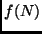 é recursivamente definida:
é recursivamente definida:
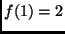 (caso base)
(caso base) -
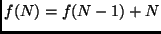 ,
para
,
para 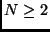 (caso recursivo)
(caso recursivo)
Exemplo 2: Torres de Hanoi
Exemplo 3: MergeSort
- Objetivo: Ordenar uma lista
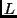 de
de 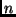 elementos.
elementos.
- Algoritmo

- Relação de Recorrência:
- Resolver uma relação de recorrência nem
sempre é fácil.
- Resolvendo uma relação de recorrência,
determina-se o tempo de execução do algoritmo recursivo
correspondente.
- Relação de recorrência:
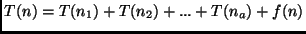 .
.
- Em geral, os
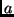 subproblemas têm o mesmo
tamanho que é uma fração de
subproblemas têm o mesmo
tamanho que é uma fração de 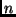 ,
digamos
,
digamos 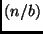 .
.
- A fórmula pode ser generalizada como:
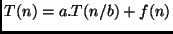
- Por exemplo, no caso do mergesort,
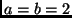 e
e 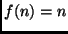 .
.
- Como resolver uma relação de recorrência:
- Método do chute e prova por indução.
- Método da árvore de recursão.
- Método do desdobramento ou iterativo.
- Método master.
Exemplo 1:
Seja a seguinte relação de recorrência,
apresentada anteriormente:
A relação de recorrência é resolvida em
duas partes:
- Chute:
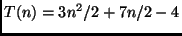 .
.
- Prova:
Como a fórmula está correta, prova-se que 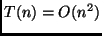 .
.
Exemplo 2:
Seja a seguinte relação de recorrência:
A relação de recorrência é resolvida em
duas partes:
- Chute:
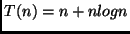 .
.
- Prova:
- Caso base:
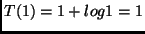 .
.
- Passo indutivo:
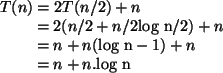
Como a fórmula está correta, prova-se que 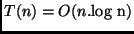 .
.
- Talvez o método mais intuitivo.
- Consiste em desenhar uma árvore cujos nós
representam os tamanhos dos correspondentes problemas.
- Cada nível
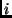 contém todos os
subproblemas de profundidade
contém todos os
subproblemas de profundidade 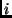 .
.
- Dois aspectos importantes:
- A altura da árvore.
- O número de passos executados de cada nível.
- A solução da recorrência (tempo de
execução do algoritmo) é a soma de todos os passos
de todos os níveis.
- No caso particular em que o total de passos de cada nível
é o mesmo,
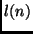 por exemplo, a solução
é:
por exemplo, a solução
é: 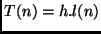 , onde
, onde 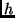 é a altura da árvore.
é a altura da árvore.
Exemplo: Mergesort: 
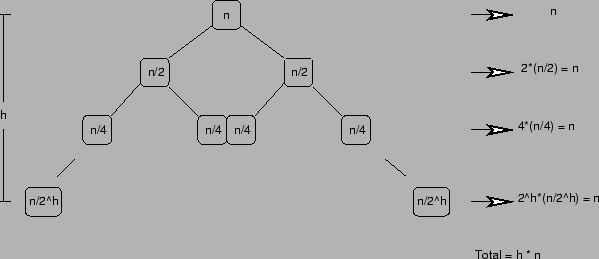
A altura da árvore é 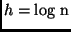 . Logo,
. Logo, 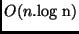 .
.
Esse método é o da árvore de recursão,
representado de forma algébrica. Consiste em:
- Usar (algumas poucas) substituições repetidamente
até encontrar um padrão.
- Escrever uma fórmmula em termos de
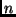 e o
número de substituições
e o
número de substituições 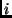 .
.
- Escolher
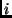 de tal forma que todas as referências
a
de tal forma que todas as referências
a  sejam referências ao caso base.
sejam referências ao caso base.
- Resolver a fórmula.
Exemplo 1: Solução da recorrência do
problema da pizza.
Vamos considerar novamente o exemplo do corte das pizzas.
A relação de recorrência é resolvida
fazendo repetidas substituições:
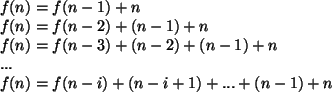
O caso base é alcançado quando 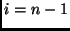 .
Logo,
.
Logo,
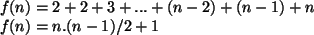
Logo 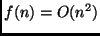 .
.
Exemplo 2: Solução da recorrência do
problema da Torre de Hanoi.
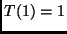
-
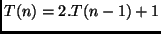 .
.
Solução por desdobramento:
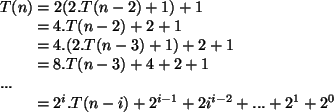
O caso base é alcançado quando 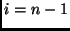 .
Logo,
.
Logo,
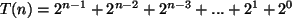
Isso é uma soma geométrica. Logo, 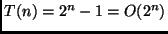
Exemplo 3: Mergesort.
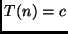
-
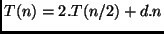 .
.
Solução por desdobramento:
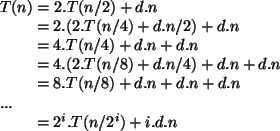
O caso base é alcançado quando 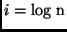 . Logo,
. Logo,
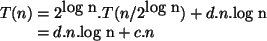
Portanto, 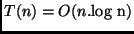
- Teorema que resolve quase todas as recorrências.
 é da forma
é da forma 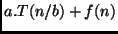 ,
, 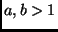 .
. - Casos:
- se
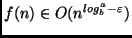 , para algum
, para algum 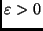 , temos que
, temos que 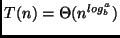 .
.
- se
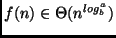 , temos que
, temos que 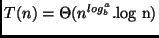 .
.
- se
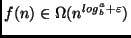 , para algum
, para algum 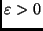 , e se
, e se 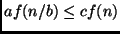 para algum
para algum 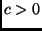 , e
, e 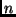 suficientemente grande, temos que
suficientemente grande, temos que 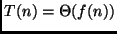 .
.
- A prova do teorema é complexa.
- Esse método é fácil de usar. Entretanto,
muitos casos são casca de banana e podemos cometer erros.
Exemplo: Mergesort: 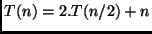
-
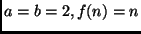 .
.
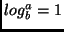 . Logo caímos no segundo
caso.
. Logo caímos no segundo
caso. -
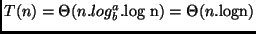
Exemplo: 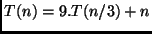
-
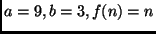 .
.
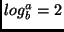 . O segundo caso não pode
ser aplicado.
. O segundo caso não pode
ser aplicado. -
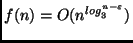 , se
, se 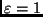 . Logo caímos no caso 1.
. Logo caímos no caso 1.
-
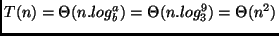
Jorge C. A. de Figueiredo 2003-11-28
![]() e
e ![]() , para
, para ![]() etc.
etc. ![]() , temos os seguintes valores de
T(n):
, temos os seguintes valores de
T(n): 
![]() cortes na pizza?
cortes na pizza? ![]() -ésimo corte
cria
-ésimo corte
cria ![]() novas fatias. Logo, o número total de
fatias obtido com
novas fatias. Logo, o número total de
fatias obtido com ![]() cortes, denotado por
cortes, denotado por ![]() ,
é dado pela seguinte relação de recorrência:
,
é dado pela seguinte relação de recorrência: ![]() é recursivamente definida:
é recursivamente definida: 


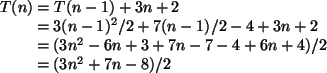
![]() .
. 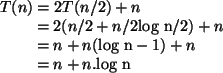
![]() .
. ![]()

![]() . Logo,
. Logo, ![]() .
. 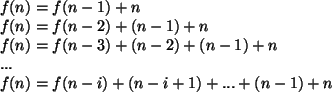
![]() .
Logo,
.
Logo, ![]()
![]() .
. 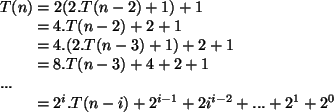
![]() .
Logo,
.
Logo, ![]()
![]()
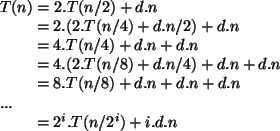
![]() . Logo,
. Logo, ![]()
![]()
![]()
![]()