Análise e Técnicas de Algoritmos
Período 2003.2
Divisão-e-Conquista
Divisão e Conquista
- Esta abordagem de concepção de algoritmos é baseada na estratégia de guerra
dos antigos romanos: dividir os inimigos e então conquistar cada pedaço
dividido.
- Na concepção de algoritmos, a idéia é pegar um problema com um tamanho de
entrada grande, dividir a entrada em pedaços menores, resolver cada pedaço e
depois combinar os resultados para obter a solução global.
- Uma questão que pode surgir: como resolver os pedaços (subproblemas) depois
da divisão? A resposta é usar divisão e conquista. O processo termina quando
temos pedaços tão pequenos que o problema se torna trivial de resolver.
- Em resumo, algoritmos que utilizam uma abordagem baseada na técnica de
divisão e conquista consistem de 3 passos básicos:
- Divisão: Dividir o problema original, em subproblemas menores.
- Conquista: Resolver cada subproblema recursivamente.
- Combinação: Combinar as soluções encontradas, compondo
uma solução para o problema original.
- Um exemplo clássico é o mergesort, algoritmo de ordenação que já foi
bastante trabalhado em nosso curso.
- Divisão: Dividir os números a serem ordenados em duas
metades.
- Conquista: Ordenar cada metade separadamente.
- Combinação: Fazer o merge das duas metades ordenadas.
- Algoritmos baseados em divisão e conquista são, em geral, recursivos.
Isso é facilmente explicado uma vez que a parte da conquista
utiliza a mesma técnica para resolver os subproblemas.
A maioria dos algoritmos de divisão e conquista divide o problema
em 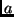 subproblemas da mesma natureza, de tamanho
subproblemas da mesma natureza, de tamanho 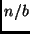 . Se
. Se 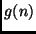 for o
tempo requerido para decompor o problema em partes iguais e depois
combinar o resultado, a complexidade de tempo pode ser determinada
pela resolução da seguinte relação de recorrência:
for o
tempo requerido para decompor o problema em partes iguais e depois
combinar o resultado, a complexidade de tempo pode ser determinada
pela resolução da seguinte relação de recorrência:
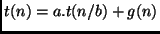 .
.
É possível utilizarmos o Teorema Master para resolver a recorrência.
Além da forma tradicional que vimos quando estudamos resolução de relação
de recorrência, o Teorema Master pode ser reescrito da seguinte forma:
Se existir um 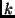 onde
onde
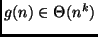 então,
então,
Existe um grande número de problemas computacionais que podem ser resolvidos
eficientemente por divisão e conquista. Na verdade, esta é uma das primeiras
técnicas (excetuando a solução ingênua ou força bruta) que é tentado para a
solução eficiente de um problema.
Entretanto, nem todos os problemas admitem uma solução eficiente por divisão
e conquista. Em alguns casos, a solução por divisão-e-conquista apresenta a
mesma complexidade assintótica de tempo que a solução ingênua. Em muitos
destes casos, porém, ainda é uma estratégia interessante:
- Requer um número menor de acessos à memória.
- São altamente paralelizáveis. Se existem vários processadores
disponíveis, a estratégia propicia eficiência.
Existem três condições que indicam que a estratégia de divisão-e-conquista
pode ser utilizada com sucesso:
- Deve ser possível decompor uma instância em sub-instâncias.
- A combinação dos resultados deve ser eficiente.
- As sub-instâncias devem ser mais ou menos do mesmo tamanho.
É possível identificar pelo menos duas situações genéricas em que a
abordagem por divisão-e-conquista é adequada:
- Problemas onde um grupo de operações são correlacionadas
ou repetidas. A multiplicação de matrizes, que veremos a seguir, é
um exemplo clássico.
- Problemas em que uma decisão deve ser tomada e, uma vez tomada, quebra o
problema em peças disjuntas. Em especial, a abordagem por divisão-e-conquiasta
é interessante quando algumas peças passam a ser irrelevantes.
O problema consiste em encontrar o maior elemento de
um array ![$A[1..n]$](img8.png) .
.
Solução Ingênua
![\begin{algorithmic}
\STATE
\STATE
\STATE $max = A[1];$\FOR{i = 2 to n}
\IF{A[i] $\rangle$\ max}
\STATE max = A[i]
\ENDIF
\ENDFOR
\end{algorithmic}](img9.png)
A solução ingênua é claramente 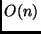 .
.
Solução por Divisão e Conquista
- Divisão: Dividir o array em duas partes (de mesmo tamanho).
- Conquista: Achar o maior valor em cada um dos sub-arrays.
- Combinação: Determinar o maior valor entre os dois valores
encontrados.
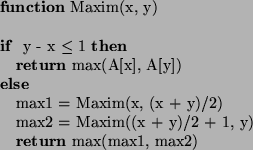
A análise do algoritmo que utiliza divisão e conquista requer a
solução da seguinte relação de recorrência:
Neste caso, 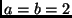 ,
,
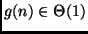 . Logo,
. Logo, 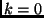 .
.
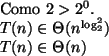
O método de divisão e conquista também produz um algoritmo
com 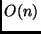 .
.
O problema consiste em encontrar o índice do elemento 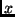 em um array ordenado.
Vamos assumir que o elemento
em um array ordenado.
Vamos assumir que o elemento 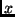 sempre existe.
sempre existe.
A solução ingênua para este problema é fazer uma busca sequencial do elemento
no array. Parar quando o elemento 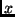 for encontrado. É trivial observar que
este algoritmo é
for encontrado. É trivial observar que
este algoritmo é 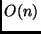 .
.
A solução por divisão e conquista:
- Divisão: Comparar com o elemento médio.
- Conquista: Buscar
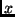 na metade esquerda ou metade direita.
na metade esquerda ou metade direita.
- Combinação: Trivial.

A análise do algoritmo que utiliza divisão e conquista requer a
solução da seguinte relação de recorrência:
-
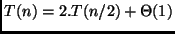 .
.
Neste caso, 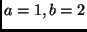 e
e 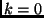 .
.
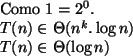
A busca binária é mais eficiente do que uma busca sequencial, quando
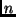 é grande.
é grande.
- O problema consiste em computar
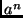 , em que
, em que 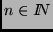 .
.
- A solução ingênua é
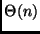
Solução Alternativa por Divisão e Conquista
A relação de recorrência é, portanto,
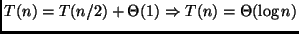 .
.
- O problema consiste em multiplicar dois números inteiros grandes.
- A multiplicação clássica (a que aprendemos fazer na escola) requer
tempo
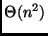 . Isso porque fazemos multiplicação dígito
a dígito.
. Isso porque fazemos multiplicação dígito
a dígito.
- A multiplicação de números grandes é bastante utilizada em criptografia.
Solução Alternativa por Divisão e Conquista
- Para evitar maiores complicações, vamos assumir que o número de dígitos
em cada número
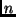 é potência de 2.
é potência de 2.
- A multiplicação de um número
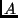 por um número
por um número 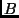 pode ser efetuada
dividindo-se o número original em dois super-dígitos e procedendo a
multiplicação, como mostrado abaixo.
pode ser efetuada
dividindo-se o número original em dois super-dígitos e procedendo a
multiplicação, como mostrado abaixo.
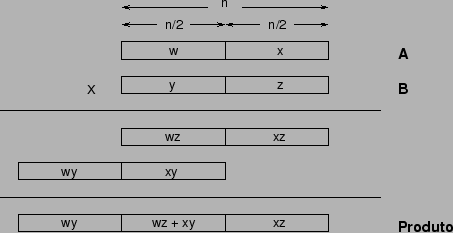
-
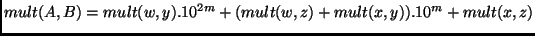
- A multiplicação por
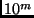 pode ser vista como o deslocamento de
pode ser vista como o deslocamento de 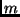 posições para a direita.
posições para a direita.
- As adições envolvidas tomam tempo
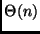 cada.
cada.
- A multiplicação de dois inteiros longos é o resultado de 4 produtos de
inteiros de tamanho metade do valor original, e um constante número de
adições e deslocamentos, com tempo
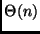 .
.
A solução por divisão e conquista:
- Divisão: Dividir cada número em dois números com metade da quantidade
de dígitos.
- Conquista: Proceder a multiplicação das quatro partes.
- Combinação: Combinar os resultados com deslocamento e adições.
A análise do algoritmo que utiliza divisão e conquista requer a
solução da seguinte relação de recorrência:
-
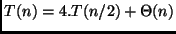 .
.
Neste caso, 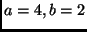 e
e 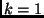 .
.
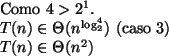
Essa solução por divisão e conquista não apresenta vantagem em relação
à solução original de multiplicação de inteiros.
Uma Solução por Divisão e Conquista Mais Eficiente
- Apesar da primeira solução por divisão e conquista não ser mais eficiente
do que a solução original, ela nos dá algumas dicas.
- Por que não temos a eficiência desejada? Ora, temos 4 multiplicaçõs
de números de tamanho
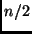 . Realmente não deve mudar nada.
. Realmente não deve mudar nada.
- A solução seria reduzir o número de multiplicações? Isso é verdade pois
sabemos que a adição e deslocamentos contribui com
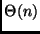 , apenas.
, apenas.
- Se observarmos mais detalhadamente, podemos reduzir para três o número de
multiplicações:
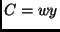 ,
, 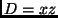 e
e 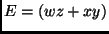 . Da seguinte forma:
. Da seguinte forma:
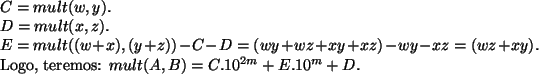
No total, fazemos 3 multiplicações, 4 adições e 2 subtrações de números com
 dígitos. É necessário ainda fazer deslocamentos mas, vimos que tudo isso
representa
dígitos. É necessário ainda fazer deslocamentos mas, vimos que tudo isso
representa 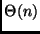 .
.
Logo, a análise do algoritmo que utiliza divisão e conquista requer a
solução da seguinte relação de recorrência:
-
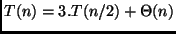 .
.
Neste caso, 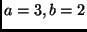 e
e 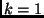 .
.
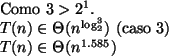
Essa solução é realmente mais eficiente? Já estudamos isso. Para 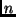 muito
grande, essa solução é muito mais eficiente.
muito
grande, essa solução é muito mais eficiente.
O algoritmo ingênuo:
![\begin{algorithmic}
\STATE
\STATE
\STATE {\bf function} MultMatriz(X, Y, Z, n)
\...
...] = X[i, j] + Y[i, k].Z[k, j]$ \ENDFOR
\ENDFOR
\ENDFOR
\STATE
\end{algorithmic}](img49.png)
Considerando que cada operação de inteiros é 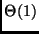 , o algoritmo
ingênuo é
, o algoritmo
ingênuo é 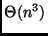 .
.
Solução Alternativa por Divisão e Conquista
- Para evitar maiores complicações, vamos assumir que
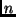 é potência de 2.
é potência de 2.
- A multiplicação de matrizes pode ser feita dividindo-se cada matriz em
quatro matrizes
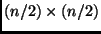 , da seguinte forma:
, da seguinte forma:
Então,
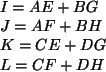
A análise do algoritmo que utiliza divisão e conquista requer a
solução da seguinte relação de recorrência:
-
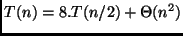 .
.
Neste caso, 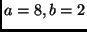 e
e 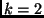 .
.
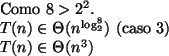
Essa solução por divisão e conquista não apresenta vantagem em relação
à solução original de multiplicação de inteiros.
Uma Solução por Divisão e Conquista Mais Eficiente
- Da mesma forma que no algoritmo da multiplicação de inteiros grandes,
seria mais eficiente se diminuíssemos o número de chamadas
recursivas.
- O Algoritmo de Strassen resolve a
multiplicação mais eficientemente da seguinte forma:
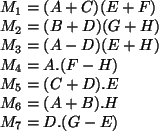
Então,
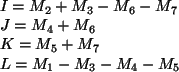
Logo, a análise do algoritmo que utiliza divisão e conquista requer a
solução da seguinte relação de recorrência:
-
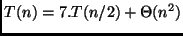 .
.
Neste caso, 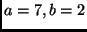 e
e 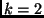 .
.
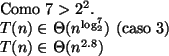
Para 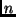 muito grande, essa solução é muito mais eficiente.
muito grande, essa solução é muito mais eficiente.
Jorge C. A. de Figueiredo
2003-12-09
![]() subproblemas da mesma natureza, de tamanho
subproblemas da mesma natureza, de tamanho ![]() . Se
. Se ![]() for o
tempo requerido para decompor o problema em partes iguais e depois
combinar o resultado, a complexidade de tempo pode ser determinada
pela resolução da seguinte relação de recorrência:
for o
tempo requerido para decompor o problema em partes iguais e depois
combinar o resultado, a complexidade de tempo pode ser determinada
pela resolução da seguinte relação de recorrência:
![]() .
.
![]() onde
onde
![]() então,
então,
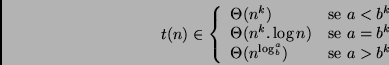
![]() .
.
![\begin{algorithmic}
\STATE
\STATE
\STATE $max = A[1];$\FOR{i = 2 to n}
\IF{A[i] $\rangle$\ max}
\STATE max = A[i]
\ENDIF
\ENDFOR
\end{algorithmic}](img9.png)
![]() .
.
![]() ,
,
![]() . Logo,
. Logo, ![]() .
.
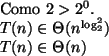
![]() .
.
![]() em um array ordenado.
Vamos assumir que o elemento
em um array ordenado.
Vamos assumir que o elemento ![]() sempre existe.
sempre existe.
![]() for encontrado. É trivial observar que
este algoritmo é
for encontrado. É trivial observar que
este algoritmo é ![]() .
.

![]() e
e ![]() .
.
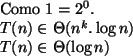
![]() é grande.
é grande.
![]() .
.

![]() e
e ![]() .
.
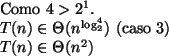
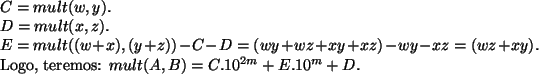
![]() dígitos. É necessário ainda fazer deslocamentos mas, vimos que tudo isso
representa
dígitos. É necessário ainda fazer deslocamentos mas, vimos que tudo isso
representa ![]() .
.
![]() e
e ![]() .
.
![]() muito
grande, essa solução é muito mais eficiente.
muito
grande, essa solução é muito mais eficiente.
![\begin{algorithmic}
\STATE
\STATE
\STATE {\bf function} MultMatriz(X, Y, Z, n)
\...
...] = X[i, j] + Y[i, k].Z[k, j]$ \ENDFOR
\ENDFOR
\ENDFOR
\STATE
\end{algorithmic}](img49.png)
![]() , o algoritmo
ingênuo é
, o algoritmo
ingênuo é ![]() .
.
![]() e
e ![]() .
.
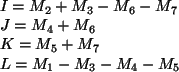
![]() e
e ![]() .
.
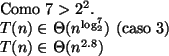
![]() muito grande, essa solução é muito mais eficiente.
muito grande, essa solução é muito mais eficiente.