Análise e Técnicas de Algoritmos
Período 2003.1

Análise de Algoritmos de Ordenação

Análise de Algoritmos de Ordenação

Formalmente, o problema da ordenação pode ser assim definido:

Entrada:

Uma seqüência de $n$ números $\langle a_1, a_2, ..., a_n \rangle$.

Saída:

Uma reordenação $\langle a\prime_1, a\prime_2, ..., a\prime_n \rangle$ da seqüência de entrada, em que $a\prime_1 \leq a\prime_2 \leq ... \leq a\prime_n$.

Em geral, consideramos a seqüência de entrada como um array de $n$ elementos.

Insertion Sort

• Um dos mais simples algoritmos de ordenação.
• Parte do array é mantida ordenada.
• O próximo número a ser considerado é colocado na posição correta na parte que já está ordenada.

A análise do algoritmo InsertionSort é muito simples e pode ser efetuada com as regras básicas para análise de algoritmos simples, apresentadas anteriormente.

É trivial observar que o algoritmo é $O(n^2)$.

MergeSort

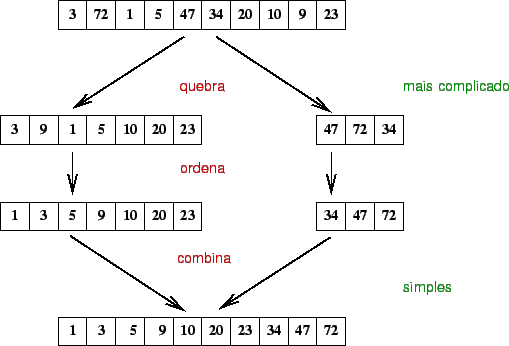
Alguns algoritmos clássicos que utilizam recursão se baseiam na estratégia de divisão-e-conquista que estudaremos mais adiante. A solução, nestes casos, pode ser definida em 3 passos:

1. Quebra a entrada original em duas partes.
2. De forma recursiva ordena cada uma das partes.
3. Combina as duas partes ordenadas, produzindo a saída ordenada.

Diferentes algoritmos recursivos foram definidos. Algumas soluções concentram os esforços na fase de quebrar o tamanho do problema, fazendo com que a fase de combinação das partes ordenadas seja simples. Outras soluções definem uma forma simples de quebrar o problema, deixando o maior esforço para a combinação dos resultados.

O mergesort faz parte dos algoritmos em que a partição é simples e a combinação é mais trabalhosa.

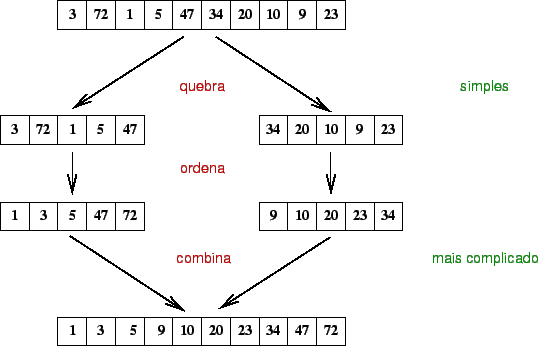
O algoritmo:

A análise do MergeSort requer a resolução de uma relação de recorrência. Para simplificação mas, sem perda de generalidade, vamos considerar $n$ como sendo uma potência de 2. Isso possibilita sempre dividir em duas partes iguais com um número par de elementos. Para $n = 1$, o tempo do mergesort é constante. Nos outros casos, o tempo de execução do algoritmo é o tempo de execução de duas chamadas recursivas com $n/2$ elementos, mais o tempo de intercalação que é linear.

A relação de recorrência é:

$$\left\{ \begin{array}{ll} \mbox{$T(n) = 1$} & \mbox{$n \leq ... ...= 2.T(n/2) + n$} & \mbox{nos demais casos} \end{array}\right.$$

Resolvendo a relação de recorrência temos:

QuickSort

Como o MergeSort, o QuickSort também é um algoritmo que utiliza a estratégia de divisão-e-conquista. Entretato, ao contrário do MergeSort, a parte mais complicada é a quebra ou partição da seqüência de entrada. A combinação das partes é trivial.

O QuickSort é talvez o algoritmo de ordenação mais usado. É fácil de implementar e muito rápido na prática.

O algoritmo:

A função de particionamento pode ser definida de diferentes formas. Por exemplo:

• Escolher o elemento mais a direita do array como sendo o pivô ($p$).
• Percorrer da esquerda para a direita até achar um elemento ($a[i]$) maior do que $p$.
• Percorre da direita para a esquerda até achar um elemento ($a[j]$) menor do que $p$.
• Trocar esses dois elementos.
• Continuar percorrendo e trocando os elementos quando pertinente até que $j \leq i$.
• Trocar $p$ com $a[i]$.

A análise do QuickSort também requer a resolução de uma relação de recorrência. Como nem sempre os dados são divididos em duas metades de igual número de elementos, é necessário fazer análise para o melhor caso, pior caso e o caso médio.

Assumindo que o tempo de partição é $O(n)$, e que a posição final do pivô é $i$, a relação de recorrência é

$$\left\{ \begin{array}{ll} \mbox{$T(n) = 1$} & \mbox{$n \leq ... ... - 1) + T(n-i)$} & \mbox{nos demais casos} \end{array}\right.$$

Algumas considerações:

O Melhor Caso

O melhor caso é quando o pivô sempre fica no meio. Nesse caso, podemos considerar que as duas partes têm a metade de elementos do problema original. Na verdade, estamos super-estimando um pouco mas isso é perfeitamente aceitável pois estamos interessados no big-oh. Logo, $T(n) = 2.T(n/2) + n$ e, como vimos no mergesort, isso indica $O(n.logn)$.

O Pior Caso

No pior caso, o pivô está sempre na primeira ou última posição:

Caso Médio

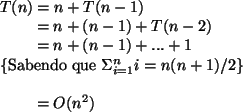
Ordenação por Comparação

Todos os algoritmos de ordenação que estudamos até agora utilizam comparação de elementos. Em uma ordenação por comparação, informação sobre a ordem relativa de dois elementos $a_i$ e $a_j$ em uma sequência é obtida utilizando testes de comparação: $a_i < a_j$, $a_i \leq a_j$, $a_i = a_j$, $a_i \geq a_j$ ou $a_i > a_j$.

É possível usar árvores de decisão para visualizar ordenação por comparação.

A figura a seguir mostra um exemplo de árvore de decisão para ordenação de uma entrada de seqüência de 3 elementos.

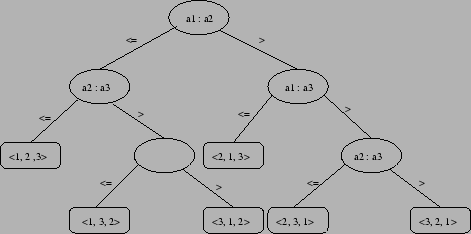
As folhas desta árvore indica uma possível ordenação para os elementos. O número de permutações possível é $n!$.

Prova de um limite inferior para o pior caso:

Para definir este limite inferior, vamos utilizar algumas propriedades de árvore:

• Uma árvore binária tem no máximo $2^d$ folhas, onde $d$ é a sua profundidade.
• Uma árvore binária com $L$ folhas tem profundidade de pelo menos $\lceil \log L \rceil$.

O caminho mais longo da raiz de uma árvore de decisão para qualquer uma de suas folhas representa o pior caso do número de comprações que o algoritmo de comparação executa (a maior profundidade de todas as folhas).

Ordenação em Tempo Linear

Counting Sort

Esse algoritmo considera que cada um dos $n$ elementos a serem ordenados é um inteiro entre $1$ e $k$. A idéia básica deste algoritmo é determinar para cada elemento de entrada $x$, o número de elementos menores do que $x$. Desta forma é possível posicionar $x$ no array de saída.

Esse algoritmo requer dois arrays auxiliares: $B[1 .. n]$ que corresponde ao array com a saída ordenada e $C[1..k]$ que provê armazenamento temporário.

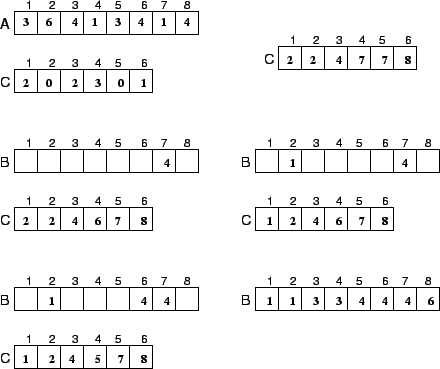
O algoritmo:

A análise deste algoritmo é trivial. O primeiro e o terceiro laços correspondem a $O(k)$, enquanto o segundo e o quarto laços são $O(n)$. O tempo total é, portanto, $O(n + k)$.

Na prática, utiliza-se CountingSort quando $k = O(n)$, proporcionando um tempo d execução $O(n)$.

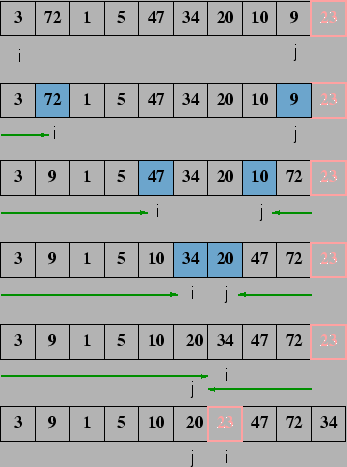
Um exemplo: