Análise e Técnicas de Algoritmos
Período 2003.1
NP-Completude
- Existem alguns problemas computacionais que são difíceis de serem
resolvidos.
- Impossível de se provar que não existe solução eficiente.
- Como definir a eficiência de uma solução?
- Vimos em nosso curso a conveniência de se utilizar medidas de
complexidade como medida de eficiência.
- Que conclusões tirar da tabela abaixo?
| Funções de Complexidade |
Tamanho da Entrada 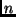 |
|
|
10 |
20 |
30 |
40 |
50 |
60 |
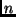 |
.00001 seg |
.00002 seg |
.00003 seg |
.00004 seg |
.00005 seg
|
.00006 seg |
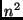 |
.0001 seg |
.0004 seg |
.0009 seg |
.0016 seg |
.0025 seg
|
.0036 seg |
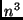 |
.001 seg |
.008 seg |
.027 seg |
.064 seg |
.125 seg |
.216 seg |
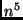 |
.1 seg |
3.2 seg |
24.3 seg |
1.7 min |
5.2 min |
13.0 min |
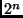 |
.001 seg |
1.0 seg |
17.9 min |
12.7 dias |
35.7 anos |
366 sec. |
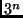 |
.059 seg |
58 min |
6.5 anos |
3855 sec. |
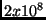 sec. sec. |
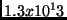 sec. sec. |
- Um algoritmo é eficiente quando a sua complexidade for polinomial
em relação ao tamanho de sua entrada.
- Um algoritmo é dito ser de tempo poliniomial se for
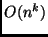 ,
para alguma constate
,
para alguma constate 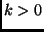 .
.
- Qualquer outro algoritmo que não for polinomial é dito ser
exponencial.
- Classificação não é absoluta.
- Algumas vezes pode ser insatisfatória mas, na maioria dos casos,
é aceitável.
- Essa definição de eficiência nos dá noção sobre intratabilidade
de problemas.
- Um problema é dito tratável se ele apresenta uma
solução polinomial.
- Um problema é intratável se ele for tão difícil que
nenhum algoritmo polinomial pode resolvê-lo.
- Alguns algoritmos polinomiais podem não ser muito úteis. Por
exemplo, se for
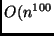 . Na prática, porém, quase sempre os polinômios
são de grau 2 ou 3.
. Na prática, porém, quase sempre os polinômios
são de grau 2 ou 3.
- Alguns problemas são tão difíceis que são indecidíveis. Por
exemplo, o problema da parada.
- Por outro lado, alguns problemas são decidíveis mas, intratáveis.
- Vamos estudar certos problemas que são, de fato, difíceis
(computacionalmente) de se resolver.
- Esse é a idéia central da teoria de NP-Completude.
- Vamos mostrar que encontrar uma solução eficiente para um certo
problema é tão difícil quanto encontrar soluções eficientes para
todos os problemas definidos em uma classe de problemas que chamamos
NP.
- Um problema algorítmico é caracterizado por:
- Conjunto de dados.
- Objetivo do problema.
- Solução.
- Problema: Encontrar um clique de tamanho
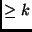 num grafo
num grafo
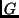 dado.
dado.
- Conjunto de dados: Um grafo
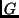 e um inteiro
e um inteiro 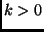 .
.
- Objetivo do problema: a própria descrição do problema.
- Problemas de Decisão: Problemas em que a saída (solução)
é SIM ou NÃO.
- Problemas de Localização: Determinar uma certa estrutura
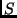 que satisfaça um conjunto de propriedades dadas.
que satisfaça um conjunto de propriedades dadas.
- Problemas de Otimização: Problemas de localização em que
as propriedades satisfazem critérios de otimização.
É possível relacionar problemas de otimização e localização com problemas de
decisão. Por exemplo:
Todos os problemas que vamos utilizar no estudo de NP-Completude são problemas
de decisão. Apesar de serem mais simples, já vimos que é possível relacionar um
problema de decisão com problemas de localização e otimização. Prova de
intratabilidade de problemas de decisão pode ser estendida aos outros casos.
O problema da satisfabilidade (SAT) é um problema de lógica que envolve
expressões booleanas. Pode ser definido da seguinte forma:
- Dados: Uma expressão booleana
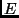 na sua forma normal conjuntiva (FNC).
na sua forma normal conjuntiva (FNC).
- Objetivo: Verificar se
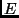 é satisfatível, ou seja, verificar se
existe uma atribuição de valores às variáveis da expressão de tal
modo que a expressão seja avaliada verdadeira.
é satisfatível, ou seja, verificar se
existe uma atribuição de valores às variáveis da expressão de tal
modo que a expressão seja avaliada verdadeira.
Uma expressão é FNC quando for uma conjunção de cláusulas. Por exemplo,
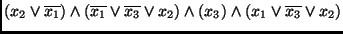 .
.
- Dados: Um grafo
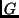 e um inteiro
e um inteiro 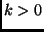 .
.
- Objetivo: Verificar se
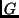 possui um conjunto independente de vértices
de tamanho
possui um conjunto independente de vértices
de tamanho 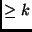 .
.
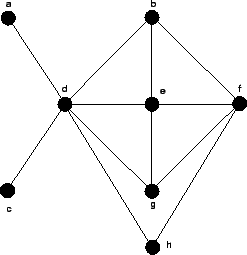
Dado um grafo 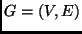 , um conjunto independente de vértices é um
subconjunto
, um conjunto independente de vértices é um
subconjunto 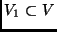 tal que qualquer par de vértices de
tal que qualquer par de vértices de 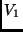 não
é adjacente. Por exemplo, na figura abaixo:
não
é adjacente. Por exemplo, na figura abaixo:
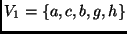 é um conjunto independente de vértices de tamanho 5.
é um conjunto independente de vértices de tamanho 5.
- Dados: Um grafo
 e um inteiro
e um inteiro 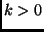 .
.
- Objetivo: Verificar se
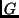 possui um clique
de tamanho
possui um clique
de tamanho 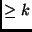 .
.
Dado um grafo 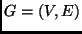 , um clique é um
subconjunto
, um clique é um
subconjunto 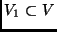 tal que qualquer par de vértices de
tal que qualquer par de vértices de 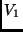 é adjacente. Por exemplo, na figura acima:
é adjacente. Por exemplo, na figura acima:
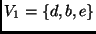 é um clique de tamanho 3.
é um clique de tamanho 3.
- Dados: Um grafo
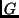 e um inteiro
e um inteiro 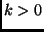 .
.
- Objetivo: Verificar se
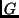 possui uma cobertura de vértices
de tamanho
possui uma cobertura de vértices
de tamanho 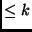 .
.
Dado um grafo 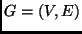 , uma cobertura de vértices é um
subconjunto
, uma cobertura de vértices é um
subconjunto 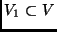 tal que qualquer aresta de vértices de
tal que qualquer aresta de vértices de 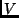 é incidente a um vértice de
é incidente a um vértice de 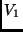 . Por exemplo, no grafo acima:
. Por exemplo, no grafo acima:
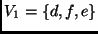 é uma cobertura de vértices de tamanho 3.
é uma cobertura de vértices de tamanho 3.
- Dados: Um grafo
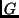 e um inteiro
e um inteiro 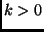 .
.
- Objetivo: Verificar se
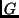 possui uma coloração com um
número
possui uma coloração com um
número 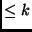 de cores.
de cores.
Dado um grafo 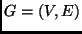 , uma coloração é uma atribuição de cores
aos vértices do grafo, de modo que dois vértices adjacentes tenham
cores distintas.
, uma coloração é uma atribuição de cores
aos vértices do grafo, de modo que dois vértices adjacentes tenham
cores distintas.
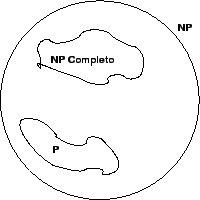
- A classe de problemas NP captura o conjunto de problemas que
acreditamos que sejam difíceis de se tratar.
- Existem, entretanto, problemas que podem ser considerados pelo
menos tão difíceis como qualquer outro em NP.
- Essa classe de problemas mais difíceis em NP é chamada de
NP-Completo ou NPC.
- O mundo NP pode ser visto como:
- No estudo de problemas NPC, faz-se necessário o conceito de
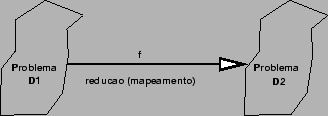
redução de problemas.
- SAT é NP-Completo.
- SAT tem a propriedade que todos os problemas em NP podem
ser reduzidos a ele, em tempo polinomial.
- Existem outros problems em NP que têm as mesmas características de
SAT.
- Se
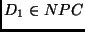 e
e 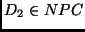 , então
, então
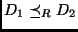 e
e
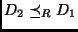 .
.
- É possível concluir:
- Se um problema NPC pode ser resolvido em tempo polinomial,
então todos os problemas de
 podem sê-lo.
podem sê-lo.
- Se um problema de NP é intratável, todos os problemas de NPC
são intratáveis.
Se
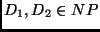 ,
, 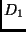 é NPC e
é NPC e
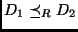 , então
, então
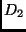 é NP-Completo.
é NP-Completo.
Para provar se um problema de decisão 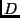 é NP-Completo, devemos seguir os seguintes passos:
é NP-Completo, devemos seguir os seguintes passos:
- Mostra que
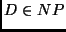 .
.
- Selecionar,
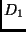 , um problema NPC conhecido.
, um problema NPC conhecido.
- Achar uma redução de
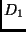 para
para 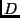 .
.
- Mostrar que a redução foi feita em tempo polinomial.
Vamos apresentar como utilizar redução para provar que alguns dos problemas
conhecidos são NPC. A figura abaixo mostra um resumo dos problemas que vamos
mostrar a prova. Cada arco denota uma redução em tempo polinomial.
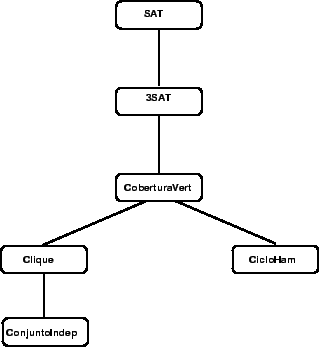
O problema 3SAT consiste em determinar o resultado de uma expressão
booleana 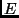 que está escrita em sua FNC é satisfatível. Cada cláusula de
que está escrita em sua FNC é satisfatível. Cada cláusula de
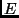 tem exatamente três literais. Por exemplo,
tem exatamente três literais. Por exemplo,
 é uma instância de 3SAT.
é uma instância de 3SAT.
Aplicando os passos para determinar se 3SAT é NPC temos:
- 3SAT é claramente NP.
- SAT é NPC. Se SAT
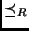 3SAT. (vamos mostrar como a redução é
feita)
3SAT. (vamos mostrar como a redução é
feita)
- Se a redução é feita em tempo polinomial, 3SAT é NPC.
Para fazer a redução, devemos substituir cada cláusula 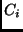 em
em 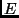 por:
por:
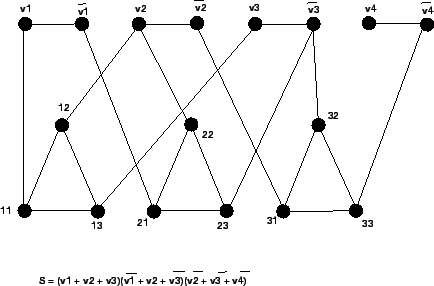
Vamos reduzir o problema 3SAT ao problema de cobertura de vértices.
- Para cada variável
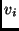 usada na fórmula
usada na fórmula 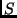 , adicionamos dois
vértices m
, adicionamos dois
vértices m 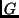 . Rotular um com
. Rotular um com 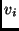 e o outro com
e o outro com
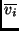 .
Adicionar ainda um arco ligando
.
Adicionar ainda um arco ligando 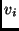 a
a
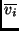 .
.
- Para cada cláusula
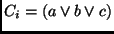 em
em 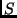 , formar um
triângulo consistindo de três vértices
, formar um
triângulo consistindo de três vértices 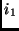 ,
, 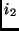 e
e 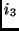 .
Adicionar arcos
.
Adicionar arcos 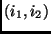 ,
, 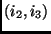 e
e 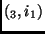 .
.
- Para cada cláusula
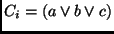 , adicionar as arestas
, adicionar as arestas
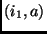 ,
, 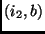 e
e 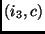 .
.
- Fazer
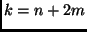 , em que
, em que 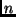 é o número de variáveis de
é o número de variáveis de 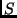 e
e 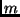 é o número de cláusulas.
é o número de cláusulas.
Jorge C. A. de Figueiredo
2003-10-02