Grafos e Algoritmos de Grafos
Muitos dos problemas estudados na teoria dos grafos podem ser utilizados na prática. Vamos apresentar alguns problemas clássicos da teoria dos grafos e que podem ser resolvidos utilizando algumas das técnicas que já aprendemos no curso.
Inicialmente, vamos introduzir alguns conceitos e a terminologia básica da teoria dos grafos.
Um grafo ![]() consiste de um conjunto de vértices,
consiste de um conjunto de vértices, ![]() ,
e um conjunto de arestas,
,
e um conjunto de arestas, ![]() . Cada aresta é um par
não ordenado de elementos distintos de
. Cada aresta é um par
não ordenado de elementos distintos de ![]() . Se
. Se ![]() é uma aresta, ela
pode ser representada por um conjunto da forma
é uma aresta, ela
pode ser representada por um conjunto da forma
![]() ou
ou ![]() ou
ou ![]() , onde
, onde ![]() . Dois vértices são adjacentes se eles formam
uma aresta. Duas arestas são adjacentes se elas têm um vértice em
comum. O grau de um vértice
. Dois vértices são adjacentes se eles formam
uma aresta. Duas arestas são adjacentes se elas têm um vértice em
comum. O grau de um vértice ![]() ,
, ![]() , é o número de arestas
que utilizam
, é o número de arestas
que utilizam ![]() em sua definição.
em sua definição.
A seguinte proposição é válida:
![]() .
.
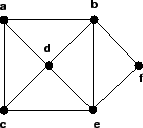
Considerando o exemplo acima, temos que:
De acordo com a nossa definição, não consideramos laços ou múltiplas arestas. Entretanto, em muitas referências a definição de grafos pode contemplar essas situações. É comum também chamar os grafos que apresentam esses elementos de pseudografo ou multigrafo.
Um grafo ![]() é dito subgrafo de
é dito subgrafo de ![]() se e somente se os conjuntos de vértices
e arestas de
se e somente se os conjuntos de vértices
e arestas de ![]() são, respectivamente, subconjuntos dos conjuntos de vértices
e arestas de
são, respectivamente, subconjuntos dos conjuntos de vértices
e arestas de ![]() .
.
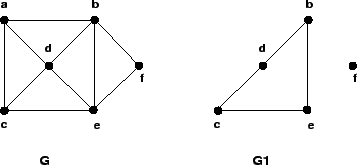
Na figura acima, ![]() é um subgrafo de
é um subgrafo de ![]() .
.
Um grafo completo é aquele em que quaisquer dois vértices de ![]() são adjacentes.
Um grafo é bipartido se o conjunto de vértices
são adjacentes.
Um grafo é bipartido se o conjunto de vértices ![]() pode ser dividido em dois conjuntos
disjuntos e não vazios
pode ser dividido em dois conjuntos
disjuntos e não vazios ![]() e
e ![]() , satisfazendo a restrição de que dois vértices
de um mesmo conjunto (
, satisfazendo a restrição de que dois vértices
de um mesmo conjunto (![]() ou
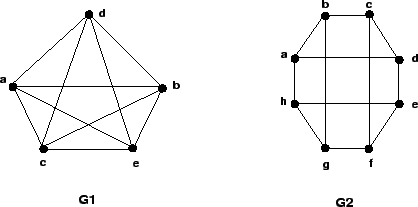
ou ![]() ) não podem ser adjacentes. Na figura abaixo,
) não podem ser adjacentes. Na figura abaixo,
![]() é um grafo completo de grau
é um grafo completo de grau ![]() e
e ![]() é um grafo bipartido.
é um grafo bipartido.
Um caminho em um grafo é uma seqüência alternada de vértices e arestas
que começa e termina com um vértice. Um caminho pode ser descrito por
uma seqüência de vértices
![]() , em que
, em que
![]() .
O tamanho de um caminho é o número de arcos no caminho que é igual a
.
O tamanho de um caminho é o número de arcos no caminho que é igual a ![]() .
Um percurso é um caminho onde
todas as arestas são distintas. Um trajeto é um caminho em que todos os
vértices são distintos. Se o primeiro vértice de um caminho ou percurso é
idêntico ao último vértice, dizemos que o caminho ou percurso é fechado.
Um percurso fechado é chamado de circuito. Um circuito onde todos os
vértices são distintos (com exceção do primeiro e do último) é chamado de
ciclo.
.
Um percurso é um caminho onde
todas as arestas são distintas. Um trajeto é um caminho em que todos os
vértices são distintos. Se o primeiro vértice de um caminho ou percurso é
idêntico ao último vértice, dizemos que o caminho ou percurso é fechado.
Um percurso fechado é chamado de circuito. Um circuito onde todos os
vértices são distintos (com exceção do primeiro e do último) é chamado de
ciclo.
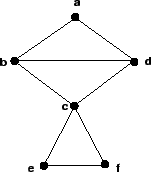
Considerando o grafo acima:
Um circuito Euleriano é aquele que contém todos os vértices e arestas de um grafo. S um grafo possui um cirduito Euleriano ele é chamado de Grafo Euleriano.
Um grafo é conectado se e somente se existir um caminho entre quaisquer dois vértices.
Teorema: Um grafo (com pelo menos dois vértices) é Euleriano se e somente se ele é conectado e todo vértice tem grau par.
O problema das pontes de Königsberg (ver figura abaixo) apresenta solução?
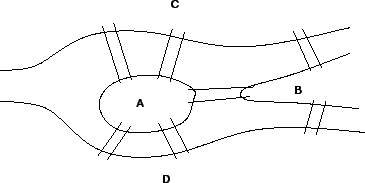
Um ciclo Hamiltoniano é aquele que contém cada um dos vértices do grafo. Se um grafo possui um ciclo Hamiltoniano ele é dito grafo Hamiltoniano.
Dígrafos ou grafos dirigidos são aqeules grafos em que cada aresta
tem uma direção. Neste caso as arestas são chamadas de arcos e são definidas
como um par ordenado de vértices distintos. Um vértice ![]() é adjacente
a
é adjacente
a ![]() se e somente se
se e somente se ![]() . Em um grafo não dirigido com aresta
. Em um grafo não dirigido com aresta
![]() ,
, ![]() é adjacente a
é adjacente a ![]() e
e ![]() é adjacente a
é adjacente a ![]() .
.
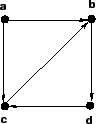
A figura acima mostra um dígrafo com 4 vértices e 5 arcos.
Um arco pode ter um terceiro componente que corresponde a um peso ou custo. Um grafo cujos arcos possuem este elemento é dito grafo ponderado ou valorado.
Os conceitos de caminho e ciclo podem ser adaptados para dígrafos, respeitando o direcinoamento definido pelos arcos. Um grafo dirigido é acíclico se ele não contém ciclos. Um grafo acíclico dirigido pode ser referenciado como DAG. Um grafo não dirigido é dito ser conectado se existe um caminho entre quaisquer dois vértices. grafo dirigido com essa propriedade é dito fortemente conectado. Se um grafo dirigido não é fortemente conectado e o correspondente grafo não dirigido é conectado, dizemos que o grafo dirigido é fracamente conectado.
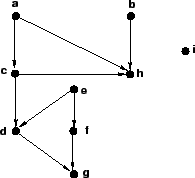
Sobre o grafo acima:
Uma árvore é um grafo não dirigido, conectado e acíclico. De forma equivalente, podemos dizer que uma árvore é um grafo que apresenta exatamente um único caminho entre qualquer par de vértices. Podemos destacar algumas propriedades básicas de árvores:
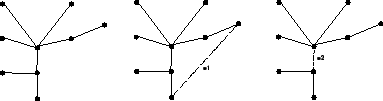
Árvores enraizadas são aquelas onde é possível distinguir um vértice especial denominado de raiz. É comum chamar os vértices de uma árvore enraizada de nós.
É importante lembrar os conceitos de:
A teoria dos grafos é uma ferramenta fundamental na área da computação. Existem centenas de problemas computacionais que podem ser resolvidos com o auxílio de grafos. Alguns exemplos clássicos são: reconhecimento de cadeias de RNA, o problema do caixeiro viajante, cliques, problemas de escalonamento, fluxo de atividades, etc.
Um exemplo de uma situação real que pode ser modelada por um grafo é o sistema de aeroportos.
Existem diferentes formas de representar um grafo ![]() . Vamos considerar
duas delas:
. Vamos considerar
duas delas:
A representação com listas de adjacência é mais utilizada porque provê
uma forma compacta de representar grafos esparsos, isto é, grafos
onde ![]() é bem menor do que
é bem menor do que ![]() .
.
A representação com matriz de adjacência é indicada no caso de grafos
densos, onde ![]() é perto de
é perto de ![]() .
.
A representação com listas de adjacência de um grafo ![]() consiste de um
array
consiste de um
array ![]() de
de ![]() listas, um para cada vértice de
listas, um para cada vértice de ![]() . Para cada
. Para cada ![]() ,
a lista de adjacência
,
a lista de adjacência ![]() contém um ponteiro para todos os vértices
contém um ponteiro para todos os vértices ![]() ,
onde existe um arco
,
onde existe um arco ![]() . Logo,
. Logo, ![]() consiste de todos os vértices
de
consiste de todos os vértices
de ![]() que são adjacentes a
que são adjacentes a ![]() . Esses vértices são armazenados em ordem
arbitrária.
. Esses vértices são armazenados em ordem
arbitrária.
A figura abaixo mostra um grafo não dirigido e sua representação com listas de adjacência.
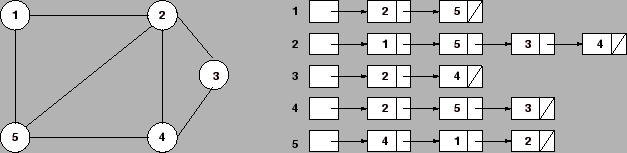
Se ![]() é um grafo dirigido, a soma dos tamanhos de todas as listas de
adjacências é
é um grafo dirigido, a soma dos tamanhos de todas as listas de
adjacências é ![]() . A figura abaixo mostra um grafo dirigido e sua representação
com listas de adjacência.
. A figura abaixo mostra um grafo dirigido e sua representação
com listas de adjacência.
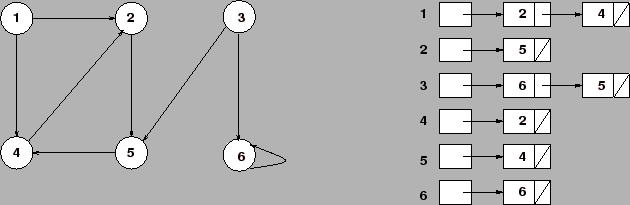
Em ambos os casos, grafos dirigidos ou não, a representação com listas de
adjacÊncia possui uma propriedade desejável que indica que a quantidade de
memória requerida é
![]() .
.
As listas de adjacência também pode ser utilizadas no caso de grafos ponderados e outras variantes de grafos.
A maior desvantagem desse método de representação é a de não possuir uma
forma eficiente de dizer se um determinado arco ![]() está presente no
grafo.
está presente no
grafo.
A representação por matriz de adjacência de um grafo ![]() requer
que os vértices sejam arbitrariamente numerados de
requer
que os vértices sejam arbitrariamente numerados de
![]() . A matriz
de adjacência de um grafo de uma matriz
. A matriz
de adjacência de um grafo de uma matriz ![]() , de ordem
, de ordem
![]() , onde
, onde
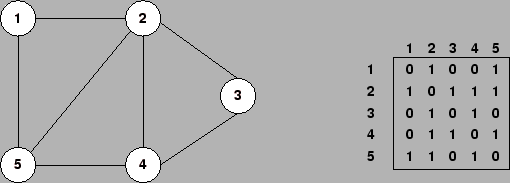
A figura abaixo mostra um grafo não dirigido e sua representação com matriz de
adjacência. Esse tipo de representação requer ![]() de memória,
independentemente do número de arcos do grafo.
de memória,
independentemente do número de arcos do grafo.
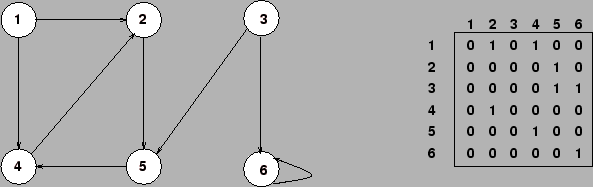
Da mesma forma, a matriz de adjacência pode ser usada para representar grafos dirigidos.
Como na representação com listas de adjacência, a matriz de adjacência pode
ser usada para representar grafos ponderados. Em vez de usar ![]() para indicar a
presença do arco, utiliza-se o peso do arco.
para indicar a
presença do arco, utiliza-se o peso do arco.
Embora a representação com lista de adjacência seja pelo menos tão eficiente quanto a representação com matriz de adjacência, a simplicidade de uma matriz de adjacência a torna preferível no caso de grafos pequenos. No caso de grafos não ponderados, a representação com matriz de adjacência tem a vantagem de requerer apenas um bit por entrada.
Existem dois tipos principais de pesquisa (caminhamento) em grafos:
A busca em amplitude representa um dos mais simples algoritmos de busca em grafo. Apesar de sua simplicidade, esse método funciona como modelo para vários importantes algoritmos de grafos como, por exemplo, o algoritmode caminho mais curto de Dijkstra e o algoritmo da árvore mínima de cobertura de Prim.
Se um grafo ![]() e um vértice inicial
e um vértice inicial ![]() . A busca em amplitude processa
os vértices por níveis, começando pelos vértices mais proóximos do vértice inicial
. A busca em amplitude processa
os vértices por níveis, começando pelos vértices mais proóximos do vértice inicial
![]() e deixando os vértices mais distantes para depois. Esse tipo de busca
é bastante similar ao caminhamento por níveis em árvores.
e deixando os vértices mais distantes para depois. Esse tipo de busca
é bastante similar ao caminhamento por níveis em árvores.
O algoritmo de busca em amplitude pode ser resumido nos seguintes passos e funciona tanto para grafos dirigidos ou não:
O algoritmo, portanto, descobre todos os vértices com distância ![]() a partir de
a partir de
![]() antes de descobrir os vértics com distância
antes de descobrir os vértics com distância ![]() .
.
Para manter controle do processamento dos vértices no algoritmo, é necessário marcar os vértices. Utilizamos um sistema de 3 cores: branca, azul e vermelha.
Como dito anteriormente, a busca em amplitude constroi uma árvore de amplitude,
inicialmente contendo apenas a raiz que é o nó de origem. Sempre que um vértice branco
![]() é descoberto a partir de um vértice já descoberto
é descoberto a partir de um vértice já descoberto ![]() , ele é adicionado
à árvore, juntamente com o arco
, ele é adicionado
à árvore, juntamente com o arco ![]() . O vértice
. O vértice ![]() é o predecessor de
é o predecessor de
![]() na árvore. Como cada vértice só é descoberto uma única vez, ele possui apenas um
predecessor.
na árvore. Como cada vértice só é descoberto uma única vez, ele possui apenas um
predecessor.
O algoritmo BFS abaixo corresponde ao algoritmo de busca por amplitude e
assume que o grafo ![]() é representado com listas de adjacência.
Para cada vértice no grafo, o algoritmo mantém estruturas auxiliares:
é representado com listas de adjacência.
Para cada vértice no grafo, o algoritmo mantém estruturas auxiliares:
![\begin{algorithmic}
\STATE {\bf BFS(G, s) }
\STATE
\FOR{$\forall u \in V[G] - \{...
...f Desenfileira(Q)}
\STATE $cor[u] = VERMELHO$\ENDWHILE
\STATE
\end{algorithmic}](img77.png)
Exemplo
O exemplo abaixo mostra a utilização do algoritmo BFS em um grafo não dirigido.
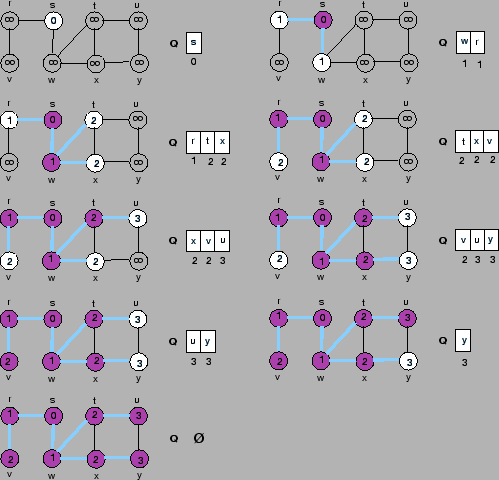
A busca em profundidade é uma generalização do caminhamento em pré-ordem.
Como o próprio nome indica, a idéia principal é buscar verticalmente
sempre que possível. Nesta estratégia, sempre que um novo vértice ![]() é
descoberto, ele deve ser explorado por completo. Quando não existe mais
nenhum vértice a ser explorado, efetua-se um bactrack para o vértice que
propiciou a descoberta de
é
descoberto, ele deve ser explorado por completo. Quando não existe mais
nenhum vértice a ser explorado, efetua-se um bactrack para o vértice que
propiciou a descoberta de ![]() .
.
Alguns detalhes do algoritmo de busca em profundidade:
![\begin{algorithmic}
\STATE {\bf DFS(G) }
\STATE
\FOR{$\forall u \in V[G]$}
\STA...
...= BRANCO$}
\STATE {\bf VisitaDFS($u$)}
\ENDIF
\ENDFOR
\STATE
\end{algorithmic}](img81.png)
![\begin{algorithmic}
\STATE {\bf VisitaDFS($u$) }
\STATE
\STATE $cor[u] \leftarro...
...ELHO$\STATE $f[u] \leftarrow tempo \leftarrow tempo + 1$\STATE
\end{algorithmic}](img82.png)
Exemplo
O exemplo a seguir, mostra o progresso da execução do algoritmo DFS sobre um grafo dirigido.
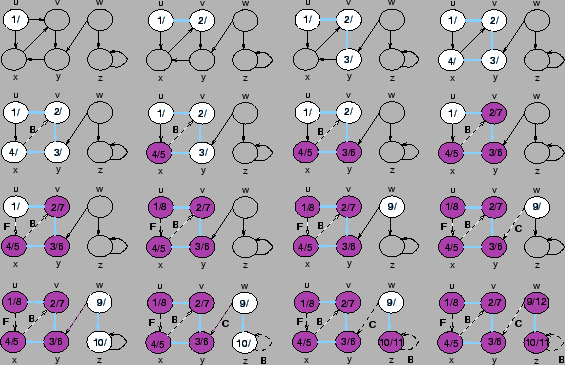
O algoritmo de busca em profundidade pode ser facilmente modificado para
classificar os tipos de arcos do grafo ![]() . Podemos distinguir 4 tipos de
arcos:
. Podemos distinguir 4 tipos de
arcos:
Essa classificação pode servir para indicar certos aspectos do grafo. Por exemplo, podemos afirmar que um grafo é acíclico se ele não possuir arcos de retorno.
A ordenação topológica pode ser vista como uma aplicação da técnica de busca em profundidade, que consiste em ordenar o conjunto de vértices de um grafo acíclico dirigido.
Podemos definir uma ordenação topológica de um grafo acíclico dirigido
![]() como uma ordenação linear de todos os vértices que satisfaz
a seguinte condição:
como uma ordenação linear de todos os vértices que satisfaz
a seguinte condição:
Secontém um arco
, então
aparece antes de
na ordenação.
O seguinte algoritmo ordena topologicamente um grafo acíclico dirigido.

Esse algoritmo é ![]() pois, o algoritmo DFS é
pois, o algoritmo DFS é ![]() e a
inserção na lista encadeada é
e a
inserção na lista encadeada é ![]() .
.
Exemplo
Grafos acíclicos dirigidos são usados em muitas aplicações para indicar precedência entre eventos. Por exemplo, a estrutura de pré-requisitos das disciplinas do Curso de Ciência da Computação na UFPB.
A ordenação topológica das disciplinas seria qualquer seqüência de disciplinas que não violasse a estrutura de pré-requisitos.
Para ilustrar a aplicação apresentada, vamos considerar a figura a seguir. Ela apresenta uma estrutura de pré-requisitos entre 9 disciplinas de um determinado curso. O tempo de inicial e final dos vértices, obtidos através do algoritmo de busca em profundidade estão também indicados.
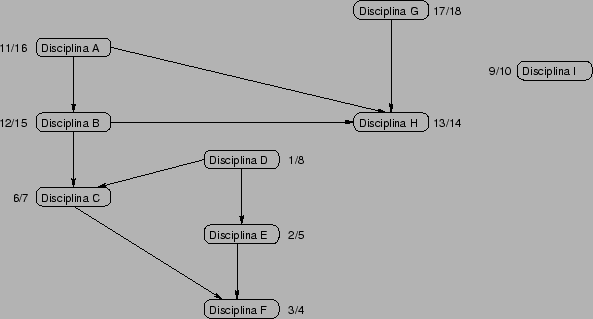
Uma possível solução para a ordenação topológica do grafo está mostrada a seguir.

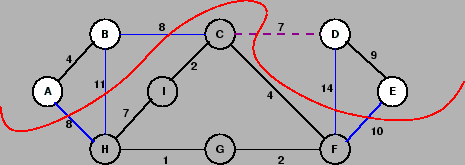
Considere um mapa modelado por um grafo: os vértices correspondem a cidades e os arcos representam estradas de terra batida entre cidades adjacentes, com os rótulos indicando a respectiva distância. O Governo do Estado planeja asfaltar algumas estradas, tornando possível sair de qualquer cidade para outra em estrada asfaltada. Que estradas deveriam ser asfaltadas, minimizando o total de asfalto a ser gasto? Esse problema na teoria dos grafos é conhecido como o problema de encontrar a árvore de cobertura mínima.
Uma árvore de cobertura de um grafo conectado ![]() é um subgrafo que forma
uma árvore e que inclui cada um dos vértices de
é um subgrafo que forma
uma árvore e que inclui cada um dos vértices de ![]() . Uma árvore de cobertura
mínima para um grafo valorado é uma árvore de cobertura em que a soma dos
pesos das arestas é mínima.
. Uma árvore de cobertura
mínima para um grafo valorado é uma árvore de cobertura em que a soma dos
pesos das arestas é mínima.
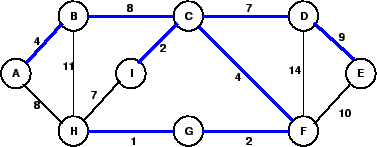
A figura acima apresenta um grafo e sua árvore de cobertura mínima (em azul).
Uma solução genérica para encontrar a árvore de cobertura mínima utiliza uma
estratégia gulosa. Em cada passo da esratégia gulosa, uma nova aresta ![]() é escolhida para compor a solução
é escolhida para compor a solução ![]() . Em cada passo,
. Em cada passo, ![]() contém um subconjunto
de alguma árvore de cobertura mínima. A nova aresta escolhida deve respeitar
essa propriedade (essa seria a nossa função de viabilidade). Dizemos,
portanto, que uma aresta que pode ser incluído no conjunto
contém um subconjunto
de alguma árvore de cobertura mínima. A nova aresta escolhida deve respeitar
essa propriedade (essa seria a nossa função de viabilidade). Dizemos,
portanto, que uma aresta que pode ser incluído no conjunto ![]() é uma aresta segura.
é uma aresta segura.
Uma solução genéria seria:

Uma forma de reconhecer uma aresta segura é:
Vamos mostrar duas formas diferentes de implementar a escolha da aresta segura.

![\begin{algorithmic}
\STATE {\bf Prim($G$, $w$, $r$)}
\STATE
\STATE $Q \leftarro...
... \STATE $chave[v] \leftarrow w(u,v)$ \ENDIF
\ENDFOR
\ENDWHILE
\end{algorithmic}](img96.png)
Considere o problema em que um motorista deseja determinar o menor caminho entre Campina Grande e Natal. Com um mapa da Região Nordeste que marca a distância entre as principais cidades, como é possível determinar o menor caminho? Uma possível solução é definir todas as rotas possíveis e selecionar aquela com a menor distância. Na verdade, essa não é uma solução interessante.
Esse problema pode ser resolvido na teoria dos grafos por algoritmos que calculam o menor caminho de origem única. Esses algoritmos podem, de fato, ser utilizados em variações de problemas de cálculo de menor caminho.
Uma forma de representar o menor caminho é utilizar dois valores ![]() e
e
![]() associados a cada um dos vértices
associados a cada um dos vértices ![]() .
. ![]() mantém o valor
da menor distância da origem até
mantém o valor
da menor distância da origem até ![]() , enquanto
, enquanto ![]() indica o vértice predecessor
de
indica o vértice predecessor
de ![]() no menor caminho encontrado.
As soluções que vamos apresentar utilizam essas duas variáveis. O algoritmo abaixo
indica como essas duas variáveis devem ser inicializadas.
no menor caminho encontrado.
As soluções que vamos apresentar utilizam essas duas variáveis. O algoritmo abaixo
indica como essas duas variáveis devem ser inicializadas. ![]() é o vértice de origem.
é o vértice de origem.
![\begin{algorithmic}
\STATE {\bf IniciaOrigemUnica($G$, $s$)}
\FOR{cada $v \in V[...
...TATE $d[v] \leftarrow \infty$\ENDFOR
\STATE $d[s] \leftarrow 0$\end{algorithmic}](img99.png)
Para encontrar o menor caminho, as variáveis ![]() e
e ![]() vão sendo ajustadas
segundo uma estratégia de relaxamento de arestas. O processo de relaxamento
consiste em testar se é possível melhorar o menor caminho.
vão sendo ajustadas
segundo uma estratégia de relaxamento de arestas. O processo de relaxamento
consiste em testar se é possível melhorar o menor caminho.
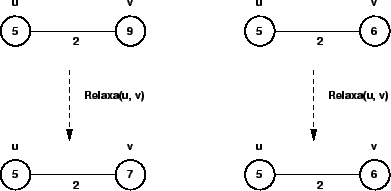
O algoritmo que executa o relaxamento em uma aresta ![]() é o seguinte:
é o seguinte:
![\begin{algorithmic}
\STATE {\bf Relaxa($u$, $v$, $w$)}
\IF{$d[v] > d[u] + w(u, v...
...\leftarrow d[u] + w(u, v)$ \STATE $\pi [v] \leftarrow u$\ENDIF
\end{algorithmic}](img102.png)
![\begin{algorithmic}
\STATE {\bf Dijkstra($G$, $w$, $s$)}
\STATE
\STATE {\bf Inic...
...dj[u]$}
\STATE {\bf Relaxa($u$, $v$, $w$)}
\ENDFOR
\ENDWHILE
\end{algorithmic}](img103.png)
